
题目列表(包括答案和解析)
1.函数f(x)=2x4-3x2+1在区间[,2]上的最大值和最小值分别是( )
A.21,- B.1,-
C.21,0 D.0,-
答案:A
(17)(本小题满分l0分)(注意:在试题卷上作答无效)
设数列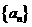 的前N项和为
的前N项和为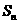 ,已知
,已知
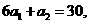 求
求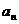 和
和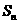
(18)△ABC的内角A、B、C的对边分别为a、b、c.己知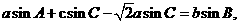
(Ⅰ)求B;
(Ⅱ)若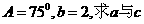
(19)
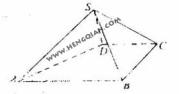 (20)如图,四棱锥
(20)如图,四棱锥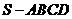 中,
中, 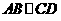 ,
,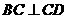 ,侧面
,侧面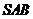 为等边三角形,
为等边三角形, 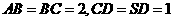 .
.
(Ⅰ)证明:SD⊥平面SAB
(Ⅱ)求AB与平面SBC所成角的大小
(21)已知函数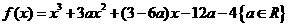
(Ⅰ)证明:曲线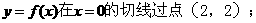
(Ⅱ)若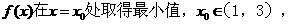 求a的取值范围。
求a的取值范围。
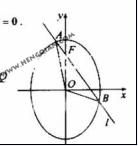
(22)已知O为坐标原点,F为椭圆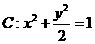 在y轴正半轴上的焦点,过F且斜率为
在y轴正半轴上的焦点,过F且斜率为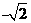 的直线
的直线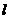 与C交与A、B两点,点P满足
与C交与A、B两点,点P满足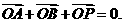
(Ⅰ)证明:点P在C上;
(Ⅱ)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上。
(13)(1-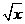 )20的二项展开式中,x的系数与x9的系数之差为: .
)20的二项展开式中,x的系数与x9的系数之差为: .
(14)已知a∈(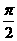 ,
,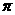 ),sinα=
),sinα=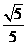 ,则tan2α=
,则tan2α=
(15)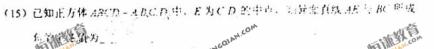
(16)已知F1、F2分别为双曲线C: 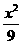 -
- 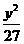 =1的左、右焦点,点A∈C,点M的坐标为(2,0),AM为∠F1AF2∠的平分线.则|AF2| = .
=1的左、右焦点,点A∈C,点M的坐标为(2,0),AM为∠F1AF2∠的平分线.则|AF2| = .
(1)设集合U=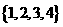 ,
,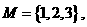
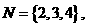 则
则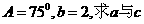
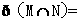
(A)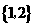 (B)
(B)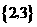 (C)
(C)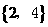 (D)
(D)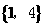 [
[
(2)函数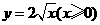 的反函数为
的反函数为
(A)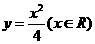 (B)
(B)
(C)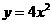
 (D)
(D)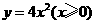
(3)权向量a,b满足a=b=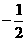 ,则
,则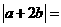
(A)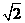 (B)
(B)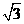 (C)
(C)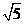 (D)
(D)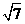
(4)若变量x、y满足约束条件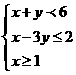 ,则
,则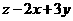 的最小值为
的最小值为
(A)17 (B)14 (C)5 (D)3
(5)(6)
(7)设函数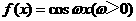 ,将
,将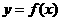 的图像向右平移
的图像向右平移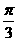 个单位长度后,所得的图像与原图像重合,则
个单位长度后,所得的图像与原图像重合,则 的最小值等于
的最小值等于
(A)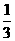 (B)
(B)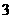 (C)
(C)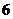 (D)
(D)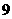
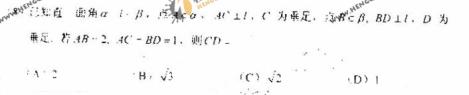
(9)曲线y=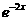 +1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为
+1在点(0,2)处的切线与直线y=0和y=x围成的三角形的面积为
(A)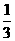 (B)
(B)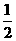 (C)
(C)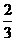 (D)1
(D)1
(10)设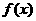 是周期为2的奇函数,当0≤x≤1时,
是周期为2的奇函数,当0≤x≤1时,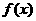 =
=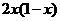 ,则
,则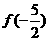 =
=
(A) -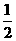 (B)
(B)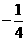 (C)
(C)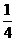 (D)
(D)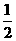
(11)设两圆 、
、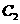 都和两坐标轴相切,且都过点(4,1),则两圆心的距离
都和两坐标轴相切,且都过点(4,1),则两圆心的距离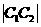 =
=
(A)4 (B)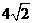 (C)8 (D)
(C)8 (D)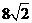
(12)已知平面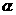 截一球面得圆M,过圆心M且与
截一球面得圆M,过圆心M且与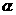 成
成 ,二面角的平面
,二面角的平面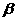 截该球面得圆N,若该球的半径为4,圆M的面积为4
截该球面得圆N,若该球的半径为4,圆M的面积为4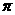 ,则圆N的面积为
,则圆N的面积为
(A)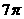 (B)
(B)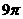 (c)
(c) (D)
(D)
第Ⅱ卷
(16)(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分)
设 是公比为正数的等比数列
是公比为正数的等比数列
(Ⅰ)求 的通项公式;
的通项公式;
(Ⅱ)设 是首项为1,公差为2的等差数列,求数列
是首项为1,公差为2的等差数列,求数列 的前
的前 项和
项和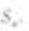 。
。
(17)(本小题满分13分,(I)小问6分,(II)小问7分)
某市公租房的房源位于A、B、C三个社区,设每位申请人只申请其中一个社区的房源,且申请其中任一个社区的房源是等可能的,求该市的任4位申请人中:
(I)没有人申请A片区房源的概率;
(II)每个片区的房源都有人申请的概率。
(18)(本小题满分13分,(I)小问7分,(II)小问6分)
设函数
(I)求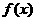 的最小正周期;
的最小正周期;
(II)若函数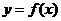 的正单位
的正单位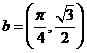 平移后得到的周函数
平移后得到的周函数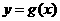 的图象,求
的图象,求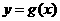 在
在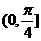 上的最大值。
上的最大值。
(19)(本小题满分12分,(Ⅰ)小题5分,(Ⅱ)小题7分)
设 的函数为
的函数为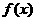 ,若函数
,若函数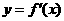 的图像关于直线
的图像关于直线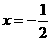 对称,且
对称,且 .
.
(Ⅰ)求实数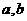 的值
的值
(Ⅱ)求函数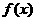 的极值
的极值
(20)(本小题满分12分,(Ⅰ)小题6分,(Ⅱ)小题6分)
如题(20)图,在四面体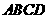 中,平面
中,平面 ,
, 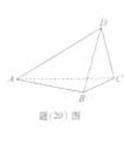
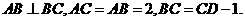
(Ⅰ)求四面体ABCD的体积;
(Ⅱ)求二面角C-AB-D的平面角的正切值。
(21)(本小题满分12分。(Ⅰ)小问4分,(Ⅱ)小问8分)
如题(21)图,椭圆的中心为原点0,离心率e=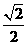 ,一条准线的方程是
,一条准线的方程是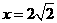
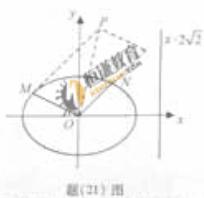
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)设动点P满足: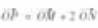 ,其中M、N是椭圆上的点,直线OM与ON的斜率之积为
,其中M、N是椭圆上的点,直线OM与ON的斜率之积为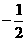 ,问:是否存在定点F,使得
,问:是否存在定点F,使得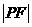 为点P到直线l:
为点P到直线l: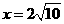 的距离之比为定值;若存在,求F的坐标,若不存在,说明理由。
的距离之比为定值;若存在,求F的坐标,若不存在,说明理由。
(11)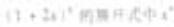 的系数是
的系数是
(12)若
(13)已原点的直线与圆 相交所得弦的
相交所得弦的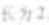 ,则该直线的方程为
,则该直线的方程为
(14)从甲、乙等10位同学中任选3位去参加某项活动,则所选3位中有甲但没有乙的概率为
(15)若实数 的最大值是
的最大值是
(1)在等差数列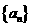 中,
中,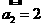 ,
,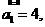 则
则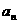 =
=
(A)12 (B)14
(C)16 (D)18
(2)设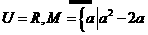 >
>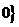 ,则
,则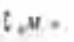
(A) 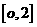 (B)
(B)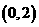
(C)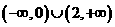 (D)
(D)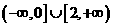
(3)曲线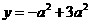 在点(1,2)处的切线方程为
在点(1,2)处的切线方程为
(A)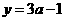 (B)
(B) 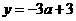
(C) 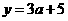 (D)
(D)
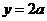
(4)
(5)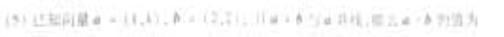
(A)1 (B)2 (C)3 (D)4
(6)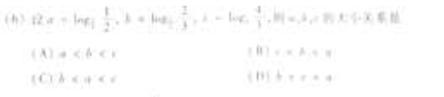
(7)若函数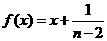
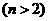 在
在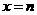 处有最小值,则
处有最小值,则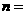
(A)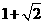 (B)
(B)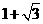 (C)3 (D)4
(C)3 (D)4
(8)若△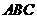 的内角
的内角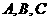 满足
满足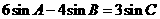 ,则
,则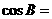
(A) 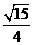 (B)
(B)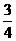
(C) 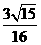 (D)
(D)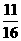
(9)设双曲线的做准线与两条渐近线交于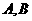 两点,左焦点为在以
两点,左焦点为在以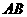 才为之直径的圆内,则该双曲线的离心率的取值范围为
才为之直径的圆内,则该双曲线的离心率的取值范围为
(A)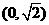 (B)
(B)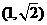
(C) 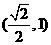 (D)
(D)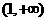
(10)高为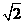 的四棱锥
的四棱锥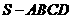 的底面是边长为1的正方形,点
的底面是边长为1的正方形,点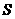 、
、 、
、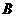 、
、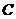 、
、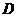 均在半径为1的同一球面上,则底面
均在半径为1的同一球面上,则底面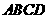 的中心与顶点
的中心与顶点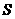 之间的 距离为
之间的 距离为
(A)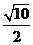 (B)
(B)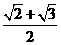 (C)
(C)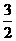 (D)
(D)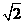
(16)(本小题满分13分)
 满足
满足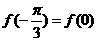 ,求函数
,求函数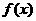 在
在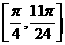 上的最大值和最小值
上的最大值和最小值
(17)(本小题满分13分。(Ⅰ)小问5分(Ⅱ)小问8分.)
 位于A.B.C三个地区,设每位申请人只申请其中一个片区的房屋,且申请其中任一个片区的房屋是等可能的,求该市的任4位申请人中:
位于A.B.C三个地区,设每位申请人只申请其中一个片区的房屋,且申请其中任一个片区的房屋是等可能的,求该市的任4位申请人中:
(Ⅰ)若有2人申请A片区房屋的概率;
(Ⅱ)申请的房屋在片区的个数的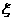 分布列与期望。
分布列与期望。
(18)(本小题满分13分。(Ⅰ)小题6分(Ⅱ)小题7分。)
设 的导数
的导数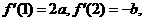 其中常数
其中常数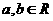 .
.
(Ⅰ)求曲线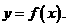 在点
在点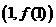 处的切线方程。
处的切线方程。
(Ⅱ)设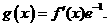 求函数
求函数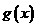 的极值。
的极值。
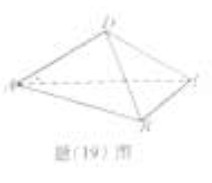
(19)本小题满分12分,(Ⅰ)小问5分, 小问7分。
如题(19)图,在四边形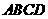 中,平面
中,平面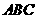 ⊥
⊥  ,
, 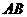 ⊥
⊥ ,
,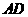 =
=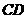 ,∠
,∠ =
=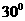
(Ⅰ)若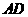 =2,
=2,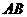 =2
=2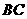 ,求四边形
,求四边形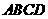 的体积。
的体积。
(Ⅱ)若二面角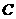 -
-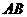 -
-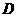 为
为 ,求异面直线
,求异面直线 与
与 所成角的余弦值。
所成角的余弦值。
(20)(本小题满分12分,第一问4分,第二问8分)
如图(20),椭圆的中心为原点O,离心率e=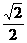 ,一条准线的方程为x=2
,一条准线的方程为x=2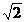 。
。
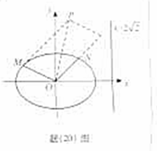 (Ⅰ)求该椭圆的标准方程。
(Ⅰ)求该椭圆的标准方程。
(Ⅱ)设动点P满足 =
=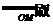 +2
+2 ,其中M,N是椭圆上的点。直线OM与ON的斜率之积为-
,其中M,N是椭圆上的点。直线OM与ON的斜率之积为-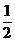 。问:是否存在两个定点
。问:是否存在两个定点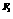 ,
,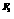 ,使得|P
,使得|P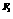 |+|P
|+|P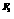 |为定值。若存在,求
|为定值。若存在,求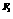 ,
,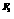 的坐标;若不存在,说明理由。
的坐标;若不存在,说明理由。
(21)(本小题满分12分。(Ⅰ)小问5分,(Ⅱ)小问7分)
设实数数列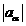 的前n项和
的前n项和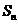 满足
满足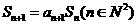
(Ⅰ)若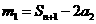 成等比数列,求
成等比数列,求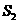 和
和
(Ⅱ)求证:
(11)在等差数列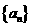 中,
中,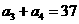 ,则
,则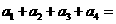
(12)已知单位向量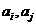 的夹角为
的夹角为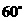 ,则
,则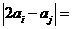
(13)将一枚均匀的硬币投掷6次,则正面出现的次数比反面出现的次数多的概率为
(14)已知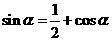 ,且
,且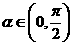 ,则
,则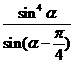 的值为
的值为
(15)设圆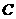 位于抛物线
位于抛物线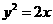 与直线
与直线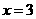 所组成的封闭区域(包含边界)内,则圆
所组成的封闭区域(包含边界)内,则圆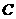 的半径??的最大值为
的半径??的最大值为
(1)复数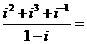
(A)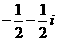 (B)
(B) 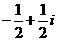
(C) 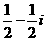 (D)
(D)
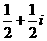
(2)“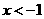 ”是“
”是“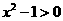 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C) 充要条件 (D)既不充分也不必要条件
(3)已知 ,则
,则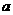 =
=
(A) -6 (B) 2 (C) 3 (D)6
(4)其中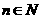 且
且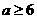 ,式中的系数相等,则
,式中的系数相等,则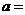
(A)6 (B)2
(C)8 (D)9
(5)下列区间中,函数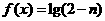 ,在其上为增函数的是
,在其上为增函数的是
(A)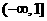 (B)
(B) 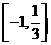
(C) 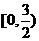 (D)(1,2)
(D)(1,2)
(6)若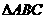 的内角
的内角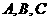 所对的边
所对的边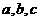 满足
满足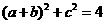 ,且
,且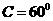 ,则
,则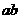 的值为
的值为
(A)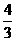 (B)
(B) 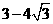
(C)1
(D) 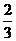
(7)已知a>0,b>0,a+b=2,则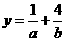 的最小值是
的最小值是
(A)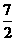 (B)4
(B)4
(C)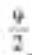 (D)5
(D)5
(8)在圆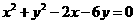 内,过点
内,过点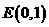 的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为
的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为
(A)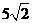 (B)
(B)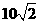

(C)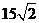 (D)
(D)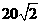
(9)高为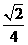 的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为
的四棱锥S-ABCD的底面是边长为1的正方形,点S、A、B、C、D均在半径为1的同一球面上,则底面ABCD的中心与顶点S之间的距离为
(A)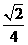 (B)
(B)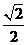
(C)1
(D)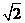
(10)设m,k为整数,方程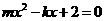 在区间(0,1)内有两个不同的根,则m+k的最小值为
在区间(0,1)内有两个不同的根,则m+k的最小值为
(A)-8 (B)8
(C)12 (D)13
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com