
题目列表(包括答案和解析)
7.若直径为2的半圆上有一点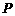 ,则点
,则点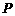 到直径两端点
到直径两端点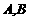
距离之和的最大值为 ▲ .
6. 函数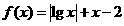 的零点个数是 ▲ .
的零点个数是 ▲ .
5. 若从集合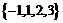 中随机取出一个数
中随机取出一个数 ,放回后再随
,放回后再随
机取出一个数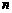 ,则使方程
,则使方程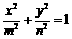 表示焦点在x轴上
表示焦点在x轴上
 的椭圆的概率为 ▲ .
的椭圆的概率为 ▲ .
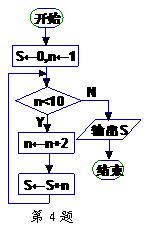
4.运行下面的一个流程图,则输出的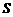 值是 ▲ .
值是 ▲ .
3.函数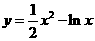 的单调递减区间为 ▲ .
的单调递减区间为 ▲ .
2.若双曲线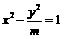 的一条渐近线方程是
的一条渐近线方程是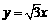 ,则
,则 等于 ▲ .
等于 ▲ .
1. 若全集
若全集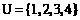 ,集合
,集合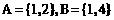 ,则
,则 ▲
.
▲
.
23.[必做题]本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
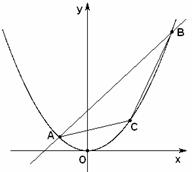
已知直线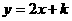 被抛物线
被抛物线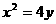 截得的弦长
截得的弦长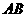 为20,
为20, 为坐标原点.
为坐标原点.
(1)求实数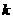 的值;
的值;
(2)问点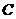 位于抛物线弧
位于抛物线弧 上何处时,△
上何处时,△ 面积最大?
面积最大?
解:(1)将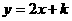 代入
代入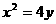 得
得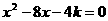 ,----------------------2分
,----------------------2分
由△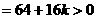 可知
可知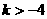 ,
,
另一方面,弦长AB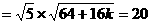 ,解得
,解得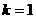 ;-------------6分
;-------------6分
(2)当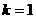 时,直线为
时,直线为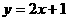 ,要使得内接△ABC面积最大,
,要使得内接△ABC面积最大,
则只须使得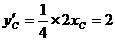 ,-----------------------------------------------8分
,-----------------------------------------------8分
即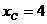 ,即
,即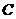 位于(4,4)点处.----------------------------------------10分
位于(4,4)点处.----------------------------------------10分
22.[必做题]本题满分10分.解答时应写出文字说明、证明过程或演算步骤.
甲、乙、丙三个同学一起参加某高校组织的自主招生考试,考试分笔试和面试两部分,笔试和面试均合格者将成为该高校的预录取生(可在高考中加分录取),两次考试过程相互独立.根据甲、乙、丙三个同学的平时成绩分析,甲、乙、丙三个同学能通过笔试的概率分别是0.6,0.5,0.4,能通过面试的概率分别是0.5,0.6,0.75.
(1)求甲、乙、丙三个同学中恰有一人通过笔试的概率;
(2)设经过两次考试后,能被该高校预录取的人数为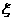 ,求随机变量
,求随机变量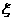 的期望
的期望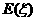 .
.
解:(1)分别记甲、乙、丙三个同学笔试合格为事件 、
、 、
、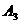 ;
;
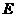 表示事件“恰有一人通过笔试”
表示事件“恰有一人通过笔试”
则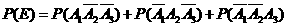
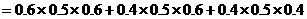
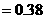 ---------------------------------------------------------------------5分
---------------------------------------------------------------------5分
(2)解法一:因为甲、乙、丙三个同学经过两次考试后合格的概率均为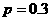 ,
,
---------------------------------------------------------------------8分
所以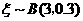 ,故
,故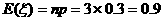 .-------------10分
.-------------10分
解法二:分别记甲、乙、丙三个同学经过两次考试后合格为事件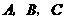 ,
,
则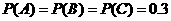
所以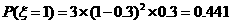 ,
,
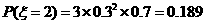 ,
,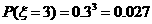 .
.
于是,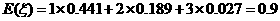 .
.
21.[选做题]本题包括A,B,C,D共4小题,请从这4题中选做2小题,每小题10分,共20分.请在答题卡上准确填涂题目标记,解答时应写出文字说明、证明过程或演算步骤.
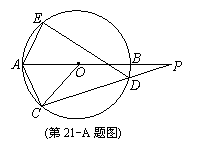 A.选修4-1:几何证明选讲
A.选修4-1:几何证明选讲
如图,⊙O的直径AB的延长线与弦CD的延长线相交于点P,E为⊙O上一点,AE=AC,求证:∠PDE=∠POC.
证明:因AE=AC,AB为直径,
故∠OAC=∠OAE. ……………………………………………………………3分
所以∠POC=∠OAC+∠OCA=∠OAC+∠OAC=∠EAC.
又∠EAC=∠PDE,
所以,∠PDE=∠POC.…………………………………………………………10分
B.选修4-2:矩阵与变换
试求曲线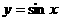 在矩阵MN变换下的函数解析式,其中M =
在矩阵MN变换下的函数解析式,其中M =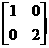 ,N =
,N =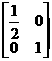
解:MN = 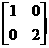
 =
=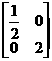 …………………………………………………4分
…………………………………………………4分
即在矩阵MN变换下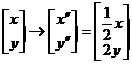 …………………………………………6分
…………………………………………6分
即曲线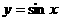 在矩阵MN变换下的函数解析式为
在矩阵MN变换下的函数解析式为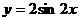 ……………10分
……………10分
C.选修4-4:坐标系与参数方程
已知直线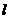 的参数方程:
的参数方程: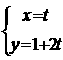 (
(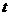 为参数)和圆
为参数)和圆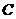 的极坐标方程:
的极坐标方程: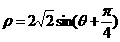 .
.
(1)将直线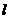 的参数方程化为普通方程,圆
的参数方程化为普通方程,圆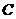 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)判断直线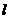 和圆
和圆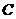 的位置关系.
的位置关系.
解:消去参数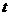 ,得直线
,得直线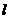 的普通方程为
的普通方程为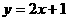 …………………………………2分
…………………………………2分
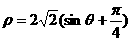 即
即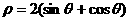 ,
,
两边同乘以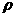 得
得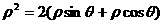 ,
,
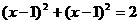 …………………………………6分
…………………………………6分
(2)圆心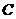 到直线
到直线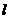 的距离
的距离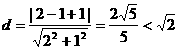 ,
,
所以直线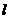 和⊙
和⊙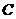 相交.
…………………………………10分
相交.
…………………………………10分
D.选修4-5:不等式选讲
已知x,y,z均为正数.求证: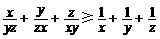 .
.
证明:因为x,y,z都是为正数,所以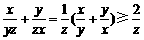 . …………………3分
. …………………3分
同理可得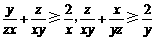 .
.
将上述三个不等式两边分别相加,并除以2,得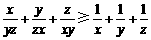 .………10分
.………10分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com