∴年产量为210吨时，可获得最大利润1 660万元．

12．某城市在发展过程中，交通状况逐渐受到大家更多的关注，据有关统计数据显示，从上午6点到中午12点，车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间的关系可近似地用如下函数给出：

y＝

求从上午6点到中午12点，通过该路段用时最多的时刻．

解：(1)当6≤t＜9时，

y′＝－t²－t+36＝－(t²+4t－96)

＝－(t+12)(t－8)．

令y′＝0，得t＝－12或t＝8.

∴当t＝8时，y有最大值．

y_max＝18.75(分钟)．

(2)当9≤t≤10时，y＝t+是增函数，

∴当t＝10时，y_max＝15(分钟)．

(3)当10＜t≤12时，y＝－3(t－11)²+18，

∴当t＝11时，y_max＝18(分钟)．

综上所述，上午8时，通过该路段用时最多，为18.75分钟．

11．某化工厂引进一条先进生产线生产某种化工产品，其生产的总成本y(万元)与年产量x(吨)之间的函数关系式可以近似地表示为y＝－48x+8 000，已知此生产线年产量最大为210吨．

(1)求年产量为多少吨时，生产每吨产品的平均成本最低，并求最低成本；

(2)若每吨产品平均出厂价为40万元，那么当年产量为多少吨时，可以获得最大利润？最大利润是多少？

解：(1)每吨平均成本为(万元)．

则＝+－48≥2 －48＝32，

当且仅当＝，即x＝200时取等号．

∴年产量为200吨时，每吨平均成本最低为32万元．

(2)设年获得总利润为R(x)万元，

则R(x)＝40x－y＝40x－+48x－8 000

＝－+88x－8 000＝－(x－220)²+1 680(0≤x≤210)．

∵R(x)在[0,210]上是增函数，

∴x＝210时，R(x)有最大值为

10．现有某种细胞100个，其中有占总数的细胞每小时分裂一次．即由1个细胞分裂成2个细胞，按这种规律发展下去，经过多少小时，细胞总数可以超过10¹⁰个？(精确到小时)(参考数据：lg3≈0.477，lg2≈0.301)

解：现有细胞100个，先考虑经过1、2、3、4个小时后的细胞总数，

1小时后，细胞总数为×100+×100×2＝×100；

2小时后，细胞总数为××100+××100×2

＝×100；

3小时后，细胞总数为××100+××100×2

＝×100；

4小时后，细胞总数为××100+××100×2

＝×100；

…

可见，细胞总数y与时间x(小时)之间的函数关系为：

y＝100×()^x，x∈N.

由100×()^x>10¹⁰，

得()^x>10⁸，

两边取以10为底的对数，得xlg>8，

∴x>，

∵≈≈45.45.

故经过46小时，细胞总数超过10¹⁰个．

9．为了保证信息安全，传输必须使用加密方式，有一种方式其加密、解密原理如下：

明文密文密文明文

已知加密为y＝a^x－2(x为明文、y为密文)，如果明文“3”通过加密后得到密文为“6”，再发送，接收方通过解密得到明文“3”，若接收方接到密文为“14”，则原发的明文是________．

解析：依题意y＝a^x－2中，当x＝3时，y＝6，故6＝a³－2，

解得a＝2.所以加密为y＝2^x－2，

因此，当y＝14时，由14＝2^x－2，解得x＝4.

答案：4

8．拟定从甲地到乙地通话m分钟的电话费由f(x)＝1.06×(0.50×[m]+1)给出，其中m>0，[m]是大于或等于m的最小整数，若通话费为10.6元，则通话时间m∈________.

解析：∵10.6＝1.06(0.50×[m]+1)，

∴0.5[m]＝9，∴[m]＝18，∴m∈(17,18]．

答案：(17,18]

7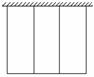．有一批材料可以建成200 m的围墙，如果用此材料在一边靠墙的地方围成一块矩形场地，中间用同样的材料隔成三个面积相等的矩形(如图所示)，则围成的矩形最大面积为______________．(围墙厚度不计)

解析：设矩形的长为x m，宽为 m，

则S＝x·＝(－x²+200x)．

当x＝100时，S_max＝2 500 m².

答案：2 500 m²

6．在养分充足的情况下，细菌的数量会以指数函数的方式增加．假设细菌A的数量每2个小时可以增加为原来的2倍；细菌B的数量每5个小时可以增加为原来的4倍．现在若养分充足，且一开始两种细菌的数量相等，要使细菌A的数量是B的数量的两倍，需要的时间为(　)

A．5 h　 　　　　　　　　　　　　　　 B．10 h

C．15 h　 　　　　　　　　　　　　　 D．30 h

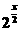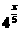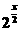解析：假设一开始两种细菌数量均为m，则依题意经过x小时后，细菌A的数量是f(x)＝m·，细菌B的数量是g(x)＝m·，令m·＝2·m·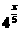，解得x＝10.

答案：B

5．汽车经过启动、加速行驶、匀速行驶、减速行驶之后停车，若把这一过程中汽车的行驶路程s看作时间t的函数，其图象可能是(　)

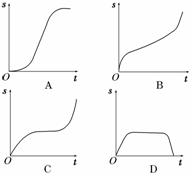
解析：画出曲线的切线，其切线的斜率的意义为速度．由图中切线斜率的变化规律可知选A.

答案：A

4．已知A、B两地相距150千米，某人开汽车以60千米/小时的速度从A地到达B地，在B地停留1小时后再以50千米/小时的速度返回A地，汽车离开A地的距离x(千米)与时间t(小时)之间的函数表达式是(　)

A．x＝60t

B．x＝60t+50t

C．x＝

D．x＝

解析：到达B地需要＝2.5小时，

所以当0≤t≤2.5时，x＝60t；

当2.5＜t≤3.5时，x＝150；

当3.5＜t≤6.5时，x＝150－50(t－3.5)．

答案：D

3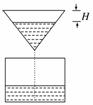．如图所示，液体从一圆锥形漏斗漏入一圆柱形桶中，开始时，漏斗盛满液体，经过3分钟漏完．已知圆柱中液面上升的速度是一个常量，H是圆锥形漏斗中液面下落的高度，则H与下落时间t(分)的函数关系表示的图象只可能是(　)

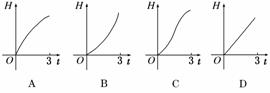
解析：由于所给的圆锥形漏斗上口大于下口，当时间取t时，漏斗中液面下落的高度不会达到漏斗高度的，对比四个选项的图象可知选B.

答案：B