1．函数y＝5^x与函数y＝－的图象关于(　)

A．x轴对称　　　　　 B．y轴对称

C．原点对称　 　　　　　　　　　　　　 D．直线y＝x对称

解析：因y＝－＝－5^－x，所以关于原点对称．

答案：C

12．已知函数f(x)＝b·a^x(其中a，b为常量，且a>0，a≠1)的图象经过点A(1,6)，B(3,24)．

(1)求f(x)；

(2)若不等式()^x+()^x－m≥0在x∈(－∞，1]时恒成立，求实数m的取值范围．

解：(1)把A(1,6)，B(3,24)代入f(x)＝b·a^x，得

结合a>0且a≠1，解得

∴f(x)＝3·2^x.

(2)要使()^x+()^x≥m在(－∞，1]上恒成立，

只需保证函数y＝()^x+()^x在(－∞，1]上的最小值不小于m即可．

∵函数y＝()^x+()^x在(－∞，1]上为减函数，

∴当x＝1时，y＝()^x+()^x有最小值.

∴只需m≤即可．

11．(2010·南京模拟)已知函数f(x)＝2^x，g(x)＝+2.

(1)求函数g(x)的值域；

(2)求满足方程f(x)－g(x)＝0的x的值．

解：(1)g(x)＝+2＝()^|x|+2，

因为|x|≥0，所以0<()^|x|≤1，即2<g(x)≤3，

故g(x)的值域是(2,3]．

(2)由f(x)－g(x)＝0得2^x－－2＝0，

当x≤0时，显然不满足方程，

即只有x>0时，满足2^x－－2＝0，

整理得(2^x)²－2·2^x－1＝0，(2^x－1)²＝2，

故2^x＝1±，

因为2^x>0，所以2^x＝1+，即x＝log₂(1+)．

10．函数y＝lg(3－4x+x²)的定义域为M，当x∈M时，求f(x)＝2^x+2－3×4^x的最值．

解：由3－4x+x²＞0，得x＞3或x＜1，

∴M＝{x|x＞3或x＜1}，

f(x)＝－3×(2^x)²+2^x+2＝－3(2^x－)²+.

∵x＞3或x＜1，∴2^x＞8或0＜2^x＜2，

∴当2^x＝，即x＝log₂时，f(x)最大，最大值为，

f(x)没有最小值．

9．已知函数y＝a^x+2－2(a>0，a≠1)的图象恒过定点A(其坐标与a无关)，则定点A的坐标为__________．

解析：当x＝－2时，无论a取何值，都有y＝－1，即图象恒过定点A(－2，－1)．

答案：(－2，－1)

8．当x∈[－2,0]时，函数y＝3^x+1－2的值域是__________．

解析：∵x∈[－2,0]时y＝3^x+1－2为增函数，

∴3^－2+1－2≤y≤3⁰⁺¹－2，即－≤y≤1.

答案：[－，1]

7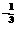．()×(－)⁰+8×－ ＝________.

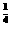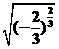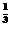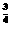解析：原式＝()×1+2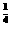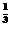×2－()＝2.

答案：2

6．已知y＝f(x+1)是定义在R上的偶函数，当x∈[1,2]时，f(x)＝2^x，设a＝f，b＝f，c＝f(1)，则a、b、c的大小关系为(　)

A．a<c<b　 　　　　　　　　　　　 B．c<b<a

C．b<c<a　 　　　　　　　　　　　 D．c<a<b

解析：由图象平移确定对称轴切入，f(x+1)是R上的偶函数⇒f(x)关于x＝1对称，而f(x)＝2^x在区间[1,2]上单调递增，则有a＝f＝f>b＝f>c＝f(1)．

答案：B

5．给出下列结论：

①当a<0时，(a²)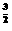＝a³；

②＝|a|(n>1，n∈N^*，n为偶数)；

③函数f(x)＝(x－2) 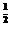－(3x－7)⁰的定义域是

{x|x≥2且x≠}；

④若2^x＝16,3^y＝，则x+y＝7.

其中正确的是(　)

A．①②　 B．②③

C．③④　 D．②④

解析：∵a<0时，(a²) 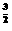>0，a³<0，∴①错；

②显然正确；解，得x≥2且x≠，∴③正确；

∵2^x＝16，∴x＝4，∵3^y＝＝3^－3，∴y＝－3，

∴x+y＝4+(－3)＝1，∴④错．故②③正确．

答案：B

4．在平面直角坐标系中，函数f(x)＝2^x+1与g(x)＝2^1－x图象关于(　)

A．原点对称　 　　　　　　　　 B．x轴对称

C．y轴对称　 　　　　　　　　　 D．直线y＝x对称

解析：y＝2^x左移一个单位得y＝2^x+1，y＝2^－x右移一个单位得y＝2^1－x，而y＝2^x与y＝2^－x关于y轴对称，

∴f(x)与g(x)关于y轴对称．

答案：C