
题目列表(包括答案和解析)
15(1).(坐标系与参数方程选做题)若曲线的极坐标方程为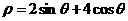 ,以极点为原点,极轴为x轴正半轴建立直角坐标系,则改曲线的直角坐标方程为
.
,以极点为原点,极轴为x轴正半轴建立直角坐标系,则改曲线的直角坐标方程为
.
答案: 。解析:做坐标系与参数方程的题,大家只需记住两点:1、
。解析:做坐标系与参数方程的题,大家只需记住两点:1、 ,2、
,2、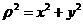 即可。根据已知
即可。根据已知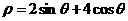 =
=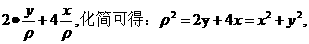
所以解析式为:

15 (2).(不等式选择题)对于实数x,y,若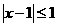 ,
,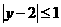 ,则
,则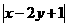 的最大值为
.
的最大值为
.
(2)此题,看似很难,但其实不难,首先解出x的范围,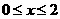 ,再解出y的范围,
,再解出y的范围,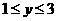 ,最后综合解出x-2y+1的范围
,最后综合解出x-2y+1的范围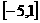 ,那么绝对值最大,就去5
,那么绝对值最大,就去5
(PS: 此题作为最后一题,有失最后一题的分量,大家从解题步骤就可看出。所以高考注重的还是基础+基础!)
14.若椭圆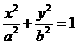 的焦点在x轴上,过点
的焦点在x轴上,过点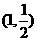 作圆
作圆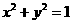 的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是
.
的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是
.
答案: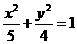 解析:设过点(1,
解析:设过点(1,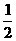 )的直线方程为:当斜率存在时,
)的直线方程为:当斜率存在时,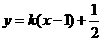 ,
,
根据直线与圆相切,圆心(0,0)到直线的距离等于半径1可以得到k=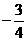 ,直线与圆方程的联立可以得到切点的坐标(
,直线与圆方程的联立可以得到切点的坐标(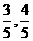 ),当斜率不存在时,直线方程为:x=1,根据两点A:(1,0),B:(
),当斜率不存在时,直线方程为:x=1,根据两点A:(1,0),B:(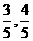 )可以得到直线:2x+y-2=0,则与y轴的交点即为上顶点坐标(2,0)
)可以得到直线:2x+y-2=0,则与y轴的交点即为上顶点坐标(2,0)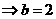 ,与x轴的交点即为焦点
,与x轴的交点即为焦点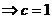 ,根据公式
,根据公式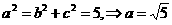 ,即椭圆方程为:
,即椭圆方程为: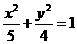
(PS:此题可能算是填空题,比较纠结的一道,因为要理清思路,计算有些繁琐。但是,是不是就做不出来呢,不是的,在我们寒假题海班的时候讲过一道与此相似的题型,也就在理科教材第147页第23题。所以最纠结的一道高考题也不过如此,你们还怕什么?)
10. 解析:s=0,n=1;带入到解析式当中,s=0+(-1)+1=0,n=2;
s=0+1+2=3, n=3;
S=3+(-1)+3=5, n=4;
S=5+1+4=10,此时s>9,输出。
(PS:此题实质是2010江苏理科卷第7题得翻版,同时在我们寒假题海班,理科讲义的第200页的第6题也讲过相似的。所以童鞋们再次遇到,应该也是灰常熟悉的。并且框图本来就是你们的拿手菜,所以最对也不觉奇怪。)
13.下图是某算法程序框图,则程序运行后输出的结果是__________.

12. 小波通过做游戏的方式来确定周末活动,他随机地往单位圆内投掷一点,若
此点到圆心的距离大于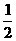 ,则周末去看电影;若此点到圆心的距离小于
,则周末去看电影;若此点到圆心的距离小于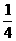 ,则去打篮球;否则,在家看书.则小波周末不在家看书的概率为
.
,则去打篮球;否则,在家看书.则小波周末不在家看书的概率为
.
答案: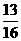 解析:方法一:不在家看书的概率=
解析:方法一:不在家看书的概率=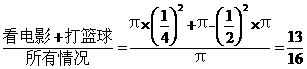
方法二:不在家看书的概率=1-在家看书的概率=1-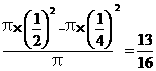
(PS: 通过生活实例与数学联系起来,是高考青睐的方向,但在我们春季班讲义二第一页的第五题已经做过类似题型,那么作为理科生,并且是上过新东方春季班课程的理科生,是不是应该作对,不解释。)
11. 已知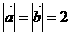 ,
,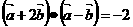 ,则
,则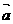 与
与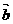 的夹角为
.
的夹角为
.
答案: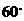 (
(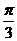 ) 解析:根据已知条件
) 解析:根据已知条件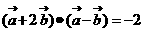 ,去括号得:
,去括号得:
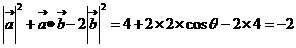 ,
, 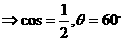
(PS:这道题其实2010年湖南文科卷的第6题翻版过来的,在我们寒假班的时候也讲过一道类似的,在文科讲义72页的第2题。 此题纯属送分题!)
(1)
若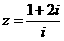 ,则复数
,则复数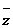 = ( )
= ( )
A.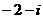 B.
B. 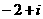 C.
C.
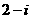 D.
D.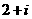
答案:C 解析: 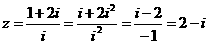
(2)
若集合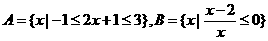 ,则
,则 = ( )
= ( )
A.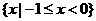 B.
B.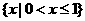 C.
C.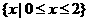 D.
D.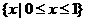
答案:B 解析: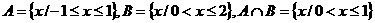
(3)
若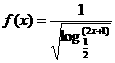 ,则
,则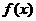 的定义域为 ( )
的定义域为 ( )
A. (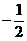 ,0)
B. (
,0)
B. (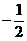 ,0] C. (
,0] C. (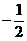 ,
, ) D. (0,
) D. (0, )
)
答案: A 解析: 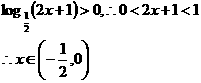
(4)
若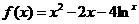 ,则
,则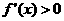 的解集为 ( )
的解集为 ( )
A. (0, )
B. (-1,0)
)
B. (-1,0)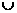 (2,
(2, )
)
C. (2, )
D. (-1,0)
)
D. (-1,0)
答案:C 解析: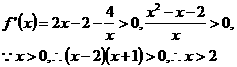
(5)
已知数列 的前
的前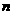 项和
项和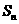 满足:
满足: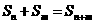 ,且
,且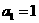 ,那么
,那么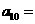 ( )
( )
A. 1 B. 9 C. 10 D. 55
答案:A 解析: 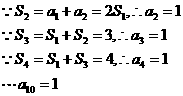
(6)
变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).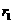 表示变量Y与X之间的线性相关系数,
表示变量Y与X之间的线性相关系数,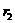 表示变量V与U之间的线性相关系数,则 ( )
表示变量V与U之间的线性相关系数,则 ( )
A.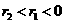 B.
B. 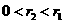 C.
C.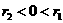 D.
D. 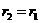
答案:C 解析: 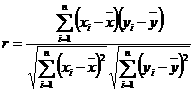 第一组变量正相关,第二组变量负相关。
第一组变量正相关,第二组变量负相关。
(7)
观察下列各式: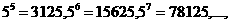 则
则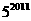 的末四位数字为 ( )
的末四位数字为 ( )
A.3125 B. 5625 C.0625 D.8125
答案:D 解析: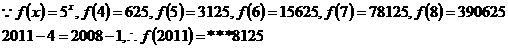
(8)
已知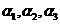 是三个相互平行的平面,平面
是三个相互平行的平面,平面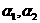 之间的距离为
之间的距离为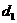 ,平面
,平面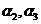 之间的距离为
之间的距离为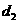 .直线
.直线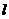 与
与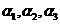 分别交于
分别交于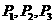 .那么
.那么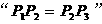 是
是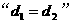 的 ( )
的 ( )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
答案:C
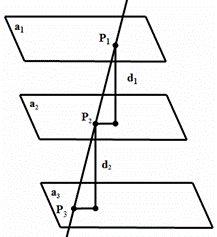 解析:平面
解析:平面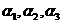 平行,由图可以得知:
平行,由图可以得知:
如果平面距离相等,根据两个三角形全等可知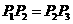
如果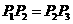 ,同样是根据两个三角形全等可知
,同样是根据两个三角形全等可知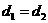
(9)
若曲线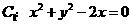 与曲线
与曲线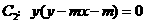 有四个不同的交点,则实数
有四个不同的交点,则实数 的取值范围是 ( )
的取值范围是 ( )
A. 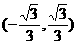 B.
B.
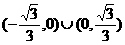
C. 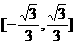 D.
D.
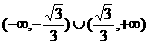
答案:B 曲线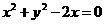 表示以
表示以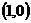 为圆心,以1为半径的圆,曲线
为圆心,以1为半径的圆,曲线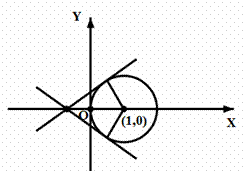
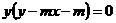 表示
表示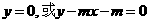 过定点
过定点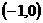 ,
,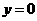 与圆有两个交点,故
与圆有两个交点,故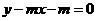 也应该与圆有两个交点,由图可以知道,临界情况即是与圆相切的时候,经计算可得,两种相切分别对应
也应该与圆有两个交点,由图可以知道,临界情况即是与圆相切的时候,经计算可得,两种相切分别对应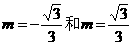 ,由图可知,m的取值范围应是
,由图可知,m的取值范围应是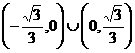
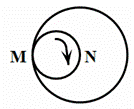
10.如右图,一个直径为1的小圆沿着直径为2的大圆内壁的逆时针方
向滚动,M和N是小圆的一条固定直径的两个端点.那么,当小圆这
样滚过大圆内壁的一周,点M,N在大圆内所绘出的图形大致是( )
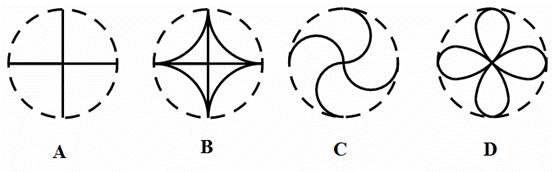
答案:A  解析:根据小圆 与大圆半径1:2的关系,找上下左右四个点,根据这四个点的位置,小圆转半圈,刚好是大圆的四分之一,因此M点的轨迹是个大圆,而N点的轨迹是四条线,刚好是M产生的大圆的半径。
解析:根据小圆 与大圆半径1:2的关系,找上下左右四个点,根据这四个点的位置,小圆转半圈,刚好是大圆的四分之一,因此M点的轨迹是个大圆,而N点的轨迹是四条线,刚好是M产生的大圆的半径。
第II卷
21. (本小题满分14分)
平面内与两定点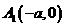 、
、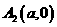 (
(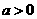 )连线的斜率之积等于非零常数m的点的轨迹,加上
)连线的斜率之积等于非零常数m的点的轨迹,加上 、
、 两点所成的曲线C可以是圆、椭圆或双曲线。
两点所成的曲线C可以是圆、椭圆或双曲线。
(I) 求曲线C的方程,并讨论C的形状与m值得关系;
(II)当m=1时,对应的曲线为 ;对给定的
;对给定的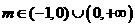 ,对应的曲线为
,对应的曲线为 。设
。设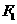 、
、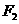 是
是 的两个焦点。试问:在
的两个焦点。试问:在 上,是否存在点N,使得
上,是否存在点N,使得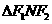 的面积
的面积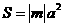 。若存在,求
。若存在,求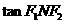 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。





20. (本小题满分13分)
设函数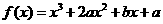 ,
,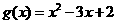 ,其中
,其中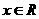 ,a、b为常数,已知曲线
,a、b为常数,已知曲线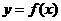 与
与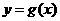 在点(2,0)处有相同的切线l。
在点(2,0)处有相同的切线l。
(I) 求a、b的值,并写出切线l的方程;
(II)若方程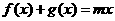 有三个互不相同的实根0、
有三个互不相同的实根0、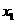 、
、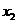 ,其中
,其中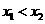 ,且对任意的
,且对任意的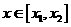 ,
,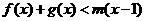 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。
18. (本小题满分12分)
如图,已知正三棱柱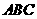 -
-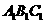 的底面边长为2,侧棱长为
的底面边长为2,侧棱长为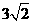 ,点E在侧棱
,点E在侧棱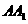 上,点F在侧棱
上,点F在侧棱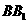 上,且
上,且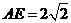 ,
,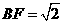 .
.
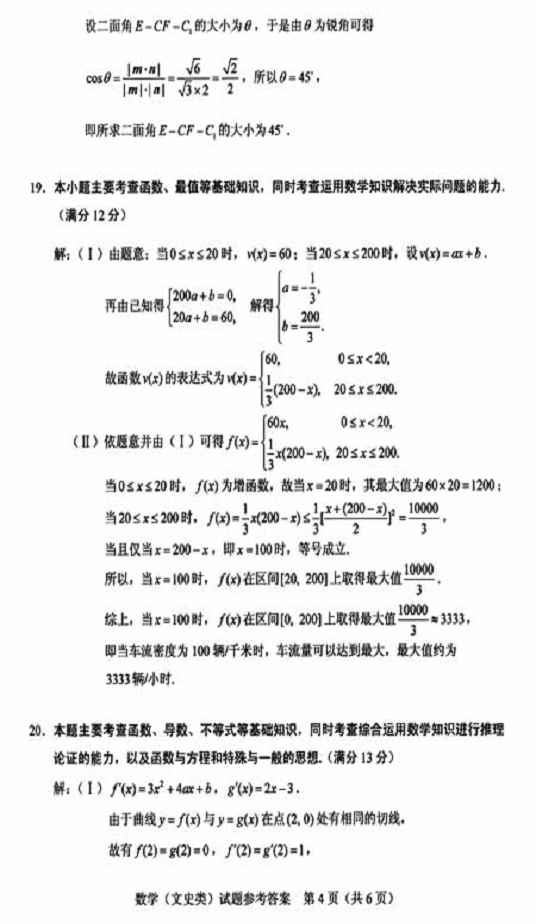
(I) 求证: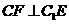 ;
;
(II) 求二面角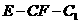 的大小。
的大小。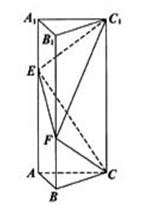
 19.
(本小题满分12分)
19.
(本小题满分12分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆 /千米)的函数,当桥上的车流魔都达到200辆 /千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆 /千米时,车流速度为60千米/小时,研究表明:当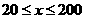 时,车流速度v是车流密度x的一次函数。
时,车流速度v是车流密度x的一次函数。
(I) 当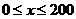 时,求函数
时,求函数 的表达式;
的表达式;
(II) 当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)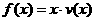 可以达到最大,并求出最大值。(精确到1辆/小时)。
可以达到最大,并求出最大值。(精确到1辆/小时)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com