10．已知函数f(x)＝x³－x²++.

证明：存在x₀∈(0，)，使f(x₀)＝x₀.

证明：令g(x)＝f(x)－x.

∵g(0)＝，g()＝f()－＝－，

∴g(0)·g()<0.

又函数g(x)在[0，]上连续，

所以存在x₀∈(0，)，使g(x₀)＝0.

即f(x₀)＝x₀.

9．已知函数f(x)＝4^x+m·2^x+1有且只有一个零点，则实数m的值为________．

解析：由题知：方程4^x+m·2^x+1＝0只有一个零点．

令2^x＝t(t>0)，

∴方程t²+m·t+1＝0只有一个正根，

∴由图象可知∴m＝－2.

答案：－2

8．若函数f(x)＝a^x－x－a(a＞0，且a≠1)有两个零点，则实数a的取值范围是________．

解析：令g(x)＝a^x(a＞0，且a≠1)，h(x)＝x+a，分0＜a＜1，a＞1两种情况．在同一坐标系中画出两个函数的图象，如图，若函数f(x)＝a^x－x－a有两个不同的零点，则函数g(x)，h(x)的图象有两个不同的交点．根据画出的图象只有当a＞1时符合题目要求．

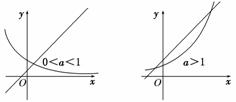
答案：(1，+∞)

7．(2011·厦门质检)若函数f(x)＝e^x+2x－6(e≈2.718)的零点属于区间(n，n+1)(n∈Z)，则n＝________.

解析：可估算两相邻自然数的函数值，f(1)＝e－4<0，f(2)＝e²－2>0，从而可知函数f(x)的零点位于区间(1,2)内，故n＝1.

答案：1

6．已知函数f(x)＝()^x－log₂x，若实数x₀是方程f(x)＝0的解，且0<x₁<x₀，则f(x₁)(　)

A．恒为正值 　　　　　　　　　 　B．等于0

C．恒为负值 　　　　　　　　　 　D．不大于0

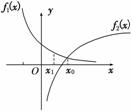解析：设f₁(x)＝()^x，f₂(x)＝log₂x，画出f₁(x)和f₂(x)的图象(如图)，易知当0<x₁<x₀时，f₁(x₁)>f₂(x₁)，所以f(x₁)＝f₁(x₁)－f₂(x₁)>0，即f(x₁)的值恒为正值．

答案：A

5．f(x)是定义在R上的以3为周期的偶函数，且f(2)＝0.则方程f(x)＝0在区间(0,6)内解的个数的最小值是(　)

A．5　 　　　　　　　　　　　　 B．4　　　　　　　　　　　　　 C．3 　　　　　　　　　 　D．2

解析：∵f(x)是定义在R上的偶函数，且周期是3，f(2)＝0，∴f(2)＝f(5)＝f(－2)＝f(1)＝f(4)＝0.

答案：B

4．若函数f(x)在(1,2)内有一个零点，要使零点的近似值满足精确度为0.01，则对区间(1,2)至少二等分(　)

A．5次　 　　　　　　　　　　　　　 B．6次

C．7次　 　　　　　　　　　　　　　 D．8次

解析：设对区间(1,2)至少二等分n次，此时区间长为1，第1次二等分后区间长为，第2次二等分后区间长为，第3次二等分后区间长为，…，第n次二等分后区间长为.依题意得<0.01，∴n>log₂100.由于6<log₂100<7，∴n≥7，即n＝7为所求．

答案：C

3．已知函数f(x)＝则函数f(x)的零点个数为(　)

A．1　 　　　　　　　　 B．2　　　　　　　　　　 C．3　 　　　　　　　　　　　　 D．4

解析：只要画出分段函数的图象，就可以知道图象与x轴有三个交点，即函数的零点有3个．

答案：C

2．设函数f(x)＝x－lnx(x＞0)，则y＝f(x)(　)

A．在区间(，1)，(1，e)内均有零点

B．在区间(，1)，(1，e)内均无零点

C．在区间(，1)内有零点，在区间(1，e)内无零点

D．在区间(，1)内无零点，在区间(1，e)内有零点

解析：∵函数f′(x)＝－，

∴x∈(3，+∞)时，y＝f(x)单调递增；

x∈(0,3)时，y＝f(x)单调递减．

而0＜＜1＜e＜3，

又f()＝+1＞0，f(1)＝＞0，f(e)＝－1＜0，

∴在区间(，1)内无零点，在区间(1，e)内有零点．

答案：D

1．函数y＝f(x)在区间(－2,2)上的图象是连续的，且方程f(x)＝0在(－2,2)上仅有一个实根0，则f(－1)·f(1)的值(　)

A．大于0　　　　B．小于0

C．等于0　 　　　　　　　　　　　 　D．无法确定

解析：由题意，知f(x)在(－1,1)上有零点0，该零点可能是变号零点，也可能是不变号零点，∴f(－1)·f(1)符号不定，如f(x)＝x²，f(x)＝x.

答案：D