4．四个不同的小球放入编号为1、2、3、4的四个盒中，则恰好有一个空盒的放法有(　)

(A)144种；(B)96种；(C)288种；(D)124种。

3．现有3个邮筒，4封信待发，不同的投记方法种数为

(A)3⁴；(B)4³；(C)P₄³；(D)C₄³。

2．若｜Z₁+Z₂｜＝｜Z₁－Z₂｜，且Z₁、Z₂、Z₁+Z₂在复平面上对应点分别为A、B、C，O为复平面原点，则四边形

OACB是(　)

(A)梯形；(B)平行四边形；(C)矩形；(D)正方形。

1．下列命题中，正确的是(　)

　(A)互为共轭复数的两数之差必是纯虚数；

(B)若Z₁²+Z₂²＝0，则Z₁=Z₂=0；

　(C)若|Z₁| +|Z₂|=0，则Z₁=Z₂=0；

　(D)任何数的偶次幂都不小于零。

17．(13分).已知ΔABC的三个顶点的坐标为A(2，-1)、B(4，3)、C(3，-2)

(1)求BC边上的高所在直线方程；

(2)求AB边的　　　 垂直平分线方程。

18(12分)解不等式 x – 1 <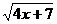

19(12分)解不等式 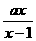　< 1　 ( a > 1)　

20(12分)求函数y = 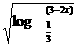　的定义域

21 (12分)　求过两条直线7x + 3y – 24 = 0 和x – y = 0的交点，且与点P(5 ，1)的距离等于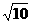的直线方程。

22(13分)如图3，设计一幅矩形宣传画，要求画面面积为4840cm²，在画面左、右各留8cm空白，上、下各留5cm空白，求：怎样设计画面的长和宽(其中长大于宽)的尺寸，能使宣传画所用的纸张面积最小？并求出这个最小值。

12．圆周上有8个等分圆周的点，以这些等分点为顶点的锐角三角形或钝角三角形的个数是　　　　　　　　 个。

11．若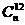=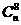，则=　　　　　　 。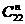

10．8个相同的足球分给6个班，每班至少1个，有　　　　　　 种分法。

9．将6本不同的书平均分成两组奖给两名同学，奖法的种数有　　　 种。

8．有不同的中文书8本，不同的英文书7本，不同的俄文书4本，从中选出不属于同一种文字的书2本，则不同的选法有　　　　　 　　　　种。