
题目列表(包括答案和解析)
8. 已知双曲线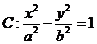 满足条件:(1)焦点为
满足条件:(1)焦点为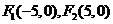 ;(2)离心率为
;(2)离心率为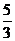 ,求得双曲线
,求得双曲线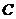 的方程为
的方程为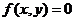 .若去掉条件(2),另加一个条件求得双曲线
.若去掉条件(2),另加一个条件求得双曲线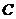 的方程仍为
的方程仍为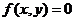 ,则下列四个条件中,符合添加的条件可以是(
)
,则下列四个条件中,符合添加的条件可以是(
)
①双曲线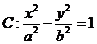 上的任意点
上的任意点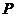 都满足
都满足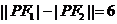 ;
;
②双曲线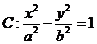 的渐近线方程为
的渐近线方程为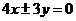 ;
;
③双曲线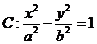 的焦距为10;
的焦距为10;
④双曲线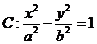 的焦点到渐近线的距离为4.
的焦点到渐近线的距离为4.
A.①③ B.②③ C.①④ D.①②④
7. 已知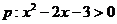 和
和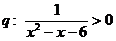 ,则
,则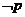 是
是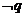 的( )
的( )
A. 充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分又不必要条件
6. 如图是一算法的程序框图,若此程序运行结果为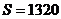 ,
,
则在判断框中应填入关于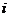 的判断条件是( )
的判断条件是( )
A. 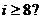 B.
B.
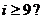
C. 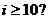 D.
D.
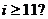
5.平面上有n条直线,它们任何两条不平行,任何三条不共点,设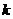 (k <n)条这样的直线把平面分成
(k <n)条这样的直线把平面分成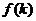 个区域,则
个区域,则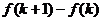 等于( )
等于( )
A. k – 1 B. k C. k +1 D. k + 2.
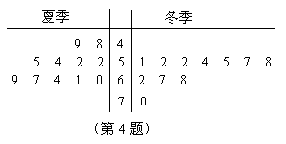
4.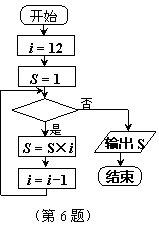 从人群中随意抽取11人,如图是这11人夏季和冬季体重情况的茎叶统计图,则夏季体重的众数与冬季体重的中位数分别是( )
从人群中随意抽取11人,如图是这11人夏季和冬季体重情况的茎叶统计图,则夏季体重的众数与冬季体重的中位数分别是( )
A. 54,55 B. 52,55 C. 52,57 D. 54,57
3.某班有学生52人,现用系统抽样的方法,抽取一个容量为4的样本,已知座位号分别为6,32,45的同学都在样本中,那么样本中另一位同学的座位号应该是( )
A . 12 B. 19 C. 27 D. 51
2. 抛物线
抛物线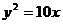 的焦点到准线的距离是( )
的焦点到准线的距离是( )
A.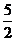 B.5 C.10
D.20
B.5 C.10
D.20
1.已知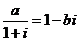 ,其中
,其中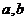 是实数,
是实数,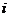 是虚数单位,则
是虚数单位,则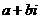 等于( )
等于( )
A. 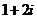 B.
B. 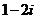 C.
C. 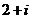 D.
D. 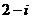
18.如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999. (Ⅰ)求p;
(Ⅱ)求电流能在M与N之间通过的概率。
(Ⅲ)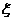 表示T1,T2,T3,T4中能通过电流的元件个数,求
表示T1,T2,T3,T4中能通过电流的元件个数,求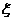 的期望.
的期望.
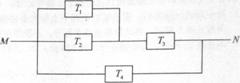
[命题意图]本试题主要考查独立事件的概率、对立事件的概率、互斥事件的概率及数学期望,考查分类讨论的思想方法及考生分析问题、解决问题的能力.
17.(14分)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°。E为线段AB的中点,将△ADE沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。
(Ⅰ)求证:BF∥平面A’DE;
(Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。

解析:本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。
(Ⅰ)证明:取A′D的中点G,连结GF,CE,由条件易知
 FG∥CD,FG=
FG∥CD,FG=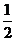 CD.BE∥CD,BE=
CD.BE∥CD,BE=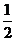 CD.
CD.
所以FG∥BE,FG=BE.
故四边形BEGF为平行四边形,所以BF∥EG
 因为
因为 平面
平面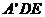 ,BF
,BF 平面
平面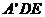
所以 BF//平面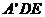
(Ⅱ)解:在平行四边形,ABCD中,设BC=a 则AB=CD=2a, AD=AE=EB=a,
连CE 因为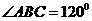 在△BCE中,可得CE=
在△BCE中,可得CE=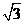 a, 在△ADE中,可得DE=a,
a, 在△ADE中,可得DE=a,
在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE, 在正三角形A′DE中,M为DE中点,所以A′M⊥DE. 由平面A′DE⊥平面BCD,
可知A′M⊥平面BCD,A′M⊥CE.取A′E的中点N,连线NM、NF,
所以NF⊥DE,NF⊥A′M., 因为DE交A′M于M,所以NF⊥平面A′DE,
则∠FMN为直线FM与平面A′DE新成角.在Rt△FMN中,NF=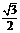 a, MN=
a, MN=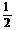 a, FM=a,
a, FM=a,
则cos =
= .所以直线FM与平面A′DE所成角的余弦值为
.所以直线FM与平面A′DE所成角的余弦值为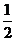 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com