
题目列表(包括答案和解析)
4.方程|x|-1=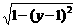 表示的曲线是
表示的曲线是
A.一个圆 B.两个半圆 C.一个半圆 D.两个圆
3.到两个坐标轴距离之差的绝对值等于2的点的轨迹是
A.2条直线 B.4条直线 C.4条射线 D.8条射线
2.直线l将圆x2+y2-2x-4y=0平分,且与直线x+2y=0垂直,则直线l的方程为
A.y=2x B.y=2x-2 C.y=-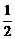 x+
x+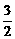 D.y=
D.y=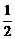 x+
x+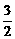
1.若命题“曲线C上的点的坐标满足方程f(x,y)=0”是正确的,则下列命题中正确的是
A.方程f(x,y)=0表示的曲线一定是曲线C
B.坐标满足方程f(x,y)=0的点一定在曲线C上
C.方程f(x,y)=0表示的曲线不一定是曲线C
D.曲线C是坐标满足方程f(x,y)=0的点的轨迹
19.设f(x)=x2-x+B,实数a满足|x-a|<1,求证:|f(x)-f(a)|<2(|a|+1).
分析:本题考查绝对值不等式|a|-|b|≤|a±b|≤|a|+|b|的应用.
证明:∵f(x)-f(a)=x2-x+B-a2+a-B=x2-a2-(x-a)=(x-a)(x+a-1),
又∵|x-a|<1,
∴|f(x)-f(a)|=|x-a|·|x+a-1|<|x+a-1|
=|x-a+2a-1|≤|x-a|+|2a-1|<1+|2a|+1=2(|a|+1).
∴|f(x)-f(a)|<2(|a|+1).
20 经过长期观测得到:在交通繁忙的时段内,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(km/h)之间的函数关系为y=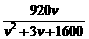 (v>0).
(v>0).
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?
分析:本题主要考查函数、不等式等基本知识,考查应用数学知识分析问题和解决问题的能力.
解:(1)依题意,y=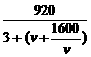 ≤
≤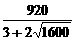 =
=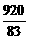 ,
,
当且仅当v=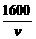 ,即v=40时,上式等号成立.
,即v=40时,上式等号成立.
所以ymax=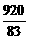 ≈11.1(千辆/小时).
≈11.1(千辆/小时).
(2)由条件得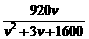 >10,
>10,
整理得v2-89v+1600<0,
即(v-25)(v-64)<0.
解得25<v<64.
答:当v=40 km/h时,车流量最大,最大车流量约为11.1千辆/小时.如果要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应大于25 km/h且小于64 km/h.
21已知a>b>0,求证: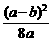 <
<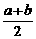 -
-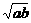 <
<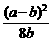 .
.
分析:本题主要考查利用分析法证明不等式.
证明:要证原不等式,只需证
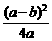 <a+b-2
<a+b-2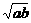 <
<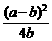
 (
(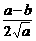 )2<(
)2<(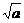 -
-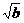 )2<(
)2<(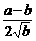 )2
)2

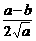 <
<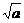 -
-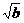 <
<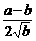

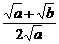 <1<
<1<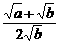
 1+
1+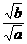 <2<
<2<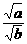 +1
+1

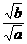 <1<
<1<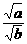

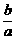 <1<
<1<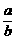 . (*)
. (*)
由题设知不等式(*)成立,以上过程可逆,原不等式成立.
15设x、y、z∈R,比较5x2+y2+z2与2xy+4x+2z-2的大小.
分析:本题考查不等式的性质与比较法.
解:(5x2+y2+z2)-(2xy+4x+2z-2)=(x-y)2+(2x-1)2+(z-1)2≥0.
∴5x2+y2+z2≥2xy+4x+2z-2
(当且仅当x=y=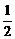 且z=1时等号成立).
且z=1时等号成立).
16.比较下列两个数的大小:
(1) 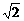 -1与2-
-1与2-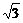 ; (2)2-
; (2)2-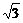 与
与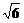 -
-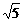 ;
;
(3)从以上两小题的结论中,你能否得出更一般的结论?并加以证明.
解法一:(变形后利用平方求差)
(1)( 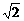 +
+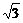 )2-(2+1)2=2
)2-(2+1)2=2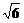 -4>0.
-4>0.
故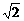 +
+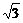 >2+1,即
>2+1,即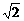 -1>2-
-1>2-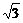 .
.
(2)(2+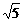 )2-(
)2-(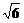 +
+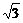 )2=4
)2=4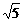 -2
-2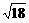 =2
=2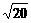 -2
-2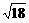 >0.
>0.
故2+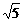 >
>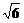 +
+ 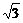 ,即2-
,即2-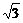 >
>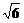 -
-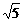 .
.
(3)一般结论:若n是正整数,
则有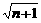 -
-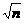 >
>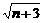 -
-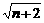 .
.
证明过程与(1)(2)类似,从略.
解法二:(利用分子有理化)
(1)∵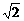 -1=
-1=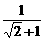 ,2-
,2-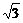 =
=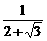 ,而
,而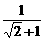 >
>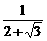 ,故
,故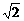 -1>2-
-1>2-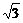 .
.
(2)∵2-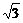 =
=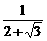 ,
, 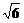 -
-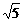 =
=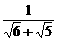 ,
,
而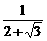 >
>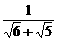 ,故2-
,故2-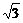 >
>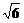 -
-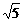 .
.
(3)同解法一.
注:本题的结论可推广到对一切n∈R+都成立.
17求证: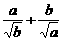 ≥
≥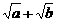 (a>0,b>0).
(a>0,b>0).
思路一:从结论入手,探求、分析上一步成立的充分条件.
证法一:(分析法)要证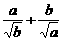 ≥
≥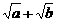 ,
,
只要证a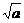 +b
+b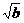 ≥a
≥a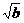 +b
+b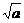 ,
,
即证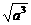 +
+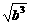 ≥
≥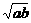 (
(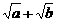 ).
).
需证(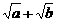 )(a-
)(a-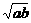 +b)≥
+b)≥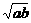 (
(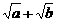 ),
),
即a-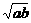 +b≥
+b≥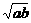 ,
,
也就是要证a+b≥2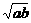 成立.a+b≥2
成立.a+b≥2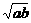 显然成立,∴原不等式成立.
显然成立,∴原不等式成立.
思路二:从条件入手,利用已知不等式,逐次推理.
证法二:(综合法)∵a、b为正实数,∴a+b≥2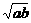 .
.
又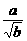 +
+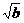 ≥2
≥2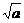 , ①
, ①
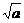 +
+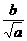 ≥2
≥2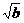 , ②
, ②
①+②得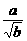 +
+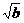 +
+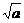 +
+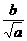 ≥2
≥2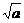 +2
+2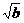 ,
,
即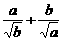 ≥
≥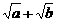 成立.
成立.
证法三:(作差比较法)
(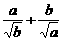 )-(
)-(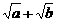 )
)
=(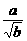 -
-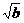 )+(
)+(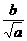 -
-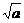 )=
)=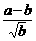 +
+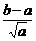
=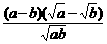
=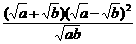 .
.
∵a、b为正实数,
∴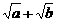 >0,
>0,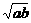 >0,(
>0,(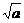 -
-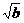 )2≥0.
)2≥0.
于是有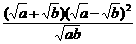 ≥0.
≥0.
∴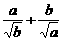 ≥
≥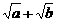 .
.
18某单位决定投资3200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米造价45元,顶部每平方米造价20元,试算:仓库底面积S的最大允许值是多少?此时铁栅长为多少?
分析:本题考查不等式在实际中的应用.
解:设铁栅长x m,一堵墙长y m,则有S=xy.
由题意得40x+2×45y+20xy=3200.
应用二元均值不等式,得3200≥2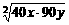 +20xy=120
+20xy=120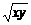 +20xy=120
+20xy=120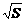 +20S.
+20S.
∴S+6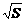 ≤160.
≤160.
∴(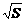 -10)(
-10)(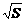 +16)≤0.
+16)≤0.
由于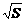 +16>0,∴
+16>0,∴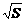 -10≤0,即S≤100.
-10≤0,即S≤100.
因此S的最大允许值是100 m2,当且仅当40x=90y,
而xy=100,解得x=15,
即铁栅的长应为15 m.
14.已知三个不等式:①ab>0;②-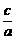 <-
<-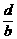 ;③bc<ad.以其中两个作为条件,余下一个作为结论,则可以组成__________个正确的命题.
;③bc<ad.以其中两个作为条件,余下一个作为结论,则可以组成__________个正确的命题.
分析:本题考查综合运用不等式的性质,证明不等式.
解:由②,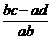 >0,又ab>0
>0,又ab>0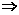 bc-ad>0,
bc-ad>0,
即bc>ad,说明由①②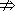 ③.同理可证明其他情况.
③.同理可证明其他情况.
答案:0
13. b g糖水中有a g糖(b>a>0),若再添上m g糖(m>0),则糖水就变甜了.试根据这个事实,提炼一个不等式:__________.
分析:本题主要考查应用数学知识解决实际问题的能力.加糖以后,糖水变甜了,说明浓度变大了.
解:加糖以前,糖水的浓度为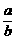 ,而加入m g糖以后,糖水浓度为
,而加入m g糖以后,糖水浓度为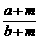 ,糖水变甜了,说明浓度变大了,即
,糖水变甜了,说明浓度变大了,即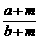 >
>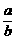 .
.
答案: 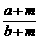 >
> 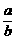
12.已知不等式:①a2+3>2a(a∈R);②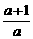 ≥2;③a5+b5>a3b2+a2b3;④a2+b2≥2(a-b-1)
≥2;③a5+b5>a3b2+a2b3;④a2+b2≥2(a-b-1)
(a,b∈R).其中正确的不等式的序号是__________.
分析:本题考查比较法,综合法证明不等式,凑平方.
解:①a2+3-2a=(a-1)2+2>0.
②a为负值不正确.
③a5+b5-a3b2-a2b3=a3(a2-b2)-b3(a2-b2)=(a3-b3)(a2-b2)=(a+b)(a-b)2(a2+ab+b2),其值大于零不一定成立.当a≠b且均为负值或一负值一零值时,其值为负值,当a=b时其值为零.不正确.
④a2+b2-2a+2b+2=(a-1)2+(b+1)2≥0.
答案:①④
11.设0<x<1,则a=2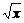 ,b=1+x,c=
,b=1+x,c=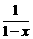 中最大的一个是__________.
中最大的一个是__________.
解析:∵b-c=(1+x)-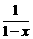 =
=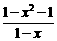
=-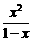 <0,
<0,
∴b<c.又b=1+x>2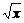 =a,∴c最大.
=a,∴c最大.
答案:c
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com