2.已知a、b∈R,则"a>b"是"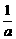<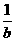"的

A.充分不必要条件

B.必要不充分条件

C.充要条件

D.既不充分也不必要条件

解析: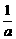-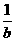=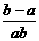<0与a>b互不能推出.

答案:D

1.已知集合M{4，7，8}，且M中至多有一个偶数，则这样的集合共有

A.3个　　　　　　　　　 B.4个　　　　　　　　　 C.6个　　　　　　　　　 D.5个

解析:集合M可以为{4，7}，{7，8}，{4}，{7}，{8}，共6个.

答案:C

19.(本小题满分12分)用分期付款方式购买家用电器一件，价格为1150元，购买当天先付150元，以后每月这一天都交付50元，并加付欠款的利息，月利率为1%，若交付150元后的第一个月开始算分期付款的第一个月，问分期付款的第十个月该交付多少钱？全部货款付清后，买这件家电实际花了多少钱？

解：购买时付了150元，欠款1000元，每月付50元，分20次付完.

设每月付款顺次组成数列{a_n}，则

a₁=50+1000×0.01=60(元).

a₂=50+(1000－50)×0.01=(60－0.5)(元).

a₃=50+(1000－50×2)×0.01=(60－0.5×2)(元).

依此类推得

a₁₀=60－0.5×9=55.5(元),

a_n=60－0.5(n－1)(1≤n≤20).

∴付款数{a_n}组成等差数列，公差d=－0.5,全部货款付清后付款总数为

S₂₀+150=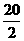(a₁+a₂₀)+150

=(2a₁+19d)×10+150

=(2×60－19×0.5)×10+150

=1255(元).

答：第十个月该交付55.5元，全部货款付清后，买这件家电实际花了1255元.

18.(本小题满分12分)已知f(x+1)=x²－4,等差数列{a_n}中，a₁=f(x－1),a₂=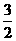－,a₃=f(x).

(1)求x的值;

(2)求a₂+a₅+a₈+…+a₂₆的值.

解：(1)∵f(x+1)=(x+1－1)²－4=［(x+1)－1］²－4，

∴f(x)=(x－1)²－4.

∴a₁=(x－2)²－4,a₃=(x－1)²－4.

又a₁+a₃=2a₂,解得x=0或x=3.

(2)∵a₁、a₂、a₃分别为0、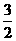－、－3或－3、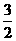－、0，

∴a_n=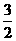－(n－1)或a_n=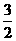(n－3).

①当a_n=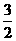－(n－1)时，a₂+a₅+…+a₂₆=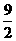(a₂+a₂₆)=;

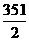②当a_n=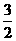 (n－3)时，a₂+a₅+…+a₂₆=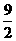(a₂+a₂₆)=.

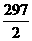17.(本小题满分12分)已知函数f(x)=ab^x的图象过点A(4,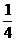)和B(5,1).

(1)求函数f(x)的解析式.

(2)记a_n=log₂f(n),n是正整数，S_n是数列{a_n}的前n项和，解关于n的不等式a_nS_n≤0.

(3)对于(2)中的a_n与S_n，整数96是否为数列{a_nS_n}中的项？若是，则求出相应的项数；若不是，则说明理由.

解：(1)由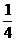=a·b⁴,1=a·b⁵,得b=4,a=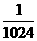,故f(x)=.

(2)由题意知a_n=log₂(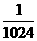·4ⁿ)=2n－10，

S_n=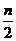(a₁+a_n)=n(n－9),

a_nS_n=2n(n－5)(n－9).

由a_nS_n≤0,得(n－5)(n－9)≤0,即5≤n≤9.

故n=5,6,7,8,9.

(3)a₁S₁=64,a₂S₂=84,a₃S₃=72,a₄S₄=40.

当5≤n≤9时，a_nS_n≤0.

当n≥10时，a_nS_n≥a₁₀S₁₀=100.

因此，96不是数列{a_nS_n}中的项.

16.(本小题满分10分)已知一元二次方程a(b－c)x²+b(c－a)x+c(a－b)=0有两个相等的实根，求证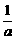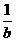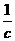：，，成等差数列.

证明：∵二次方程有等根,

∴Δ=b²(c－a)²－4ac(b－c)(a－b)=0.

∴b²c²+a²b²+(2ac)²－4a²bc－4abc²+2ab²c=0.

∴(ab+bc－2ac)²=0.

∴ab+bc－2ac=0.

∴b(a+c)=2ac.

∴=+.

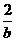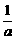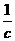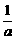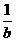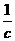∴,,成等差数列.

注：本题也可这样做：∵x=1是方程的根，

∴x₁=x₂=1.

∴x₁x₂=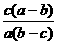=1.

∴2ac=ab+bc.∵abc≠0,

∴=+.

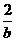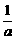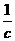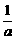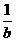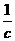∴,,成等差数列.

15.(本小题满分8分)在等差数列{a_n}中，a₁=－60,a₁₇=－12.

(1)求通项a_n;

(2)求此数列前30项的绝对值的和.

解：(1)a₁₇=a₁+16d,即－12=－60+16d,∴d=3.

∴a_n=－60+3(n－1)=3n－63.

(2)由a_n≤0,则3n－63≤0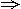n≤21.∴|a₁|+|a₂|+…+|a₃₀|=－(a₁+a₂+…+a₂₁)+(a₂₂+a₂₃+…+a₃₀)=(3+6+9+…+60)+(3+6+…+27)=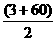×20+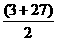×9=765.

14.已知a₁=－,a_n=a_n－1+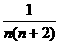(n∈N^*,n≥2),则a_n=_________.

解析：a_n=a_n－1+,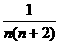

a_n－1=a_n－2+,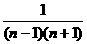

a_n－2=a_n－3+,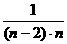

……

a₂=a₁+.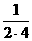

相加得a_n=a₁+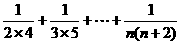

=－［()+()+…+()］

=－.

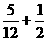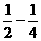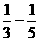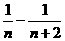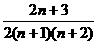答案：－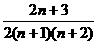

13.若△ABC三边a,b,c成等差数列，并且a²,b²,c²也成等差数列，则a,b,c的大小关系为_________.

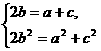
由①得c=2b－a,代入②整理得a²－2ab+b²=0.

∴a=b.

答案：a=b=c

12.在等差数列{a_n}中，若a₁+3a₈+a₁₅=120,则2a₉－a₁₀=________.

解析：∵{a_n}是等差数列，

∴a₁+3a₈+a₁₅=5a₈=120,即a₈=24.

又∵{a_n}是等差数列，∴a₈+a₁₀=2a₉.

∴2a₉－a₁₀=a₈=24.

答案：24