
题目列表(包括答案和解析)
17.(本小题满分12分)设a∈R,函数f(x)=x2+|x-a|+1,x∈R,求f(x)的最小值.
解:(1)当x≥a时,f(x)=x2+x-a+1
=(x+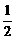 )2-a+
)2-a+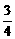 ,
,
若a≤-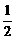 时,则f(x)在[a,+∞)上的最小值为f(-
时,则f(x)在[a,+∞)上的最小值为f(-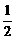 )=
)=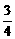 -a;
-a;
若a>-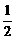 时,则f(x)在[a,+∞)上单调递增,
时,则f(x)在[a,+∞)上单调递增,
f(x)min=f(a)=a2+1.
(2)当x≤a时,f(x)=x2-x+a+1=(x-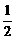 )2+a+
)2+a+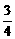 ];
];
若a≤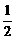 时,则f(x)在(-∞,a]上单调递减,f(x)min=f(a)=a2+1;
时,则f(x)在(-∞,a]上单调递减,f(x)min=f(a)=a2+1;
当a>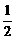 时,则f(x)在(-∞,a]上的最小值为f(
时,则f(x)在(-∞,a]上的最小值为f(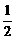 )=
)=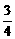 +a.
+a.
综上所述,当a≤-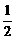 时,f(x)的最小值为
时,f(x)的最小值为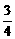 -a;
-a;
当-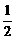 <a≤
<a≤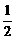 时,f(x)的最小值为a2+1;
时,f(x)的最小值为a2+1;
当a>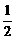 时,f(x)的最小值为
时,f(x)的最小值为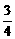 +a.
+a.
16.(本小题满分10分)若二次函数f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,且f(-2)>f(3),设m>-n>0,试比较f(m)和f(n)的大小,并说明理由.
解:∵f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,
∴对任意x∈R,恒有f(-x)=f(x),
即a(-x)2+b(-x)+c=ax2+bx+c恒成立.
∴2bx=0对任意x∈R恒成立.
∴b=0.∴f(x)=ax2+c.
∵f(-2)>f(3),且f(-2)=f(2),
∴f(2)>f(3).∴a<0.
∴f(x)在(0,+∞)上是减函数.
又∵m>-n>0,
∴f(m)<f(-n).
而f(-n)=f(n),
∴f(m)<f(n).
15.(本小题满分8分)如图,动点P从边长为4的正方形ABCD顶点B开始,顺次经过C、D、A绕周界一圈,设x表示P的行程,y表示△APB的面积,求函数y=f(x)的解析式.

解:设PB=x,∵AB=4,由三角形面积公式,得
y=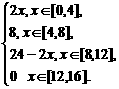
14.已知f(x)是R上的增函数,A(0,-1),B(3,1)是其图象上的两个点,那么|f(x+1)|<1的解集是_________.
解析:|f(x+1)|<1即-1<f(x+1)<1,
∴f(0)<f(x+1)<f(3).
∵f(x)在R上单调递增,
∴0<x+1<3.
∴-1<x<2.
答案:{x|-1<x<2}
13.对于定义在R上的函数f(x),若实数x0满足f(x0)=x0,则称x0是函数f(x)的一个不动点.若函数f(x)=x2+ax+1没有不动点,则实数a的取值范围是_______.
解析:f(x)无不动点等价于方程x2+ax+1=x无解,
即(a-1)2-4<0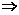 -1<a<3.
-1<a<3.
答案:-1<a<3
12.如果f[f(x)]=2x-1,则一次函数f(x)=_________.
解析:用待定系数法求函数解析式.
设f(x)=ax+b(a≠0),则
f[f(x)]=af(x)+b=a(ax+b)+b
=a2x+ab+b.
由f[f(x)]=2x-1,得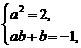
解得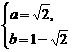 或
或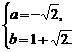
所以f(x)=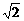 x+1-
x+1-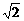 ,或f(x)=-
,或f(x)=- 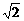 x+1+
x+1+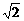 .
.
答案: 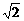 x+1-
x+1-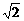 或-
或-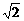 x+1+
x+1+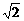
11.已知函数f(x)= 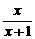 ,则f(1)+f(2)+…+f(2002)+f(2003)+f(1)+f(
,则f(1)+f(2)+…+f(2002)+f(2003)+f(1)+f(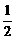 )+…+f(
)+…+f( )+f(
)+f( )=_______.
)=_______.
解析:∵f(x)+f(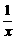 )=
)=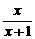 +
+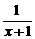 =1,
=1,
∴原式=2003×1=2003.
答案:2003
10.定义在R上的函数y=f(x-1)是单调递减函数(如下图所示),给出四个结论,其中正确结论的个数是
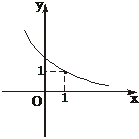
①f(0)=1 ②f(1)<1 ③f-1(1)=0
④f--1(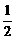 )>0
)>0
A.1 B.2 C.3 D.4
解析:由图知,当x=1时,f(x-1)=1,即f(0)=1.
∴①正确.
∵y=f(x)的反函数存在,
∴f--1(1)=0.
∴③正确.
由题意知x=2时,f(x-1)<1,即f(1)<1.
∴②正确.
∵y=f(x-1)单调递减,
∴y=f--1(x)单调递减.
由图知, 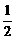 <f(0),
<f(0),
∴f--1(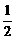 )>f--1[f(0)]=0.
)>f--1[f(0)]=0.
∴④正确.
答案:D
第Ⅱ卷(非选择题 共70分)
9.已知函数y=f(x)(x∈[a,b]),那么集合{(x,y)|y=f(x),x∈[a,b]}∩{(x,y)|x=2}中所含元素的个数为
A.1 B.0 C.0或1 D.1或2
解析:此题即求y=f(x)(x∈[a,b])与直线x=2的交点个数,不注意对应法则常误选A,其原因在于未注意2是否属于[a,b].若2∈[a,b],则交点为1个;若2 [a,b],则交点为0个.
[a,b],则交点为0个.
答案:C
8.函数f(x)=x+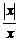 的图象是
的图象是

解析:f(x)=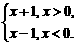
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com