
题目列表(包括答案和解析)
15已知平面α∥β,AB、CD为夹在α、β间的异面线段,E、F分别为AB、CD的中点.求证:EF∥α,EF∥β.
分析:要证EF∥α,根据线面平行的判定定理,只需在α内找一条直线与EF平行;或过EF作一平面,使该平面与α平行,据面面平行的性质定理即可证得.
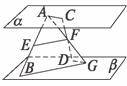
证法一:
连结AF并延长交β于G?.
∵AG∩CD=F,
∴AG、CD确定平面γ,且γ∩α=AC,γ∩β=DG.
∵α∥β,∴AC∥DG.∴∠ACF=∠GDF.
又∠AFC=∠DFG,CF=DF,
∴△ACF≌△GDF.∴AF=FG.
又AE=BE,∴EF∥BG.
∵BG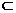 β,∴EF∥β.
β,∴EF∥β.
同理,FE∥α.
证法二:∵AB与CD为异面直线,∴A CD.
CD.
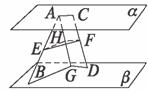
在A、C、D确定的平面内过点A作AG∥CD交β于点G,取AG的中点H,连结AC、HF.
∵α∥β,∴AC∥DG∥FH.
∵DG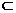 β,∴HF∥β.
β,∴HF∥β.
又∵E为AB的中点,
∴EH∥BG.∴EH∥β.
又EH∩HF=H,∴平面EHF∥β.
∵EF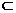 平面EHF,∴EF∥β.同理,EF∥α.
平面EHF,∴EF∥β.同理,EF∥α.
16如果两个平面分别平行于第三个平面,那么这两个平面互相平行.
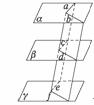
答案:已知:α∥β,γ∥β,
求证:α∥γ.
证明:如图,作两个相交平面分别与α,β,γ交于a,c,e和b,d,f.
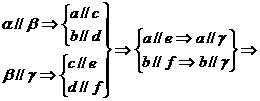 α∥γ.
α∥γ.
17如图所示,A,B,C,D四点在平面M和N之外,它们在M内的射影A1,B1,C1,D1成一直线,在N内的射影A2,B2,C2,D2组成一个平行四边形,求证:ABCD是平行四边形.
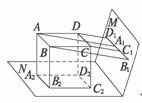
证明:∵A,B,C,D四点在平面M内的射影是一条直线,
∴ABCD为平面四边形.
又AA2⊥平面N,DD2⊥平面N,
∴AA2∥DD2.
∵A2B2∥C2D2,
∴平面AA2B2B∥平面CC2D2D.
又ABCD为平面四边形,
∴AB∥CD.
同理可证AD∥BC.
∴ABCD为平行四边形.
18如图,正方体ABCD-A1B1C1D1的棱长为a,过其对角线BD1的平面分别与AA1、CC1相交于点E,F,求截面四边形BED1F面积的最小值.
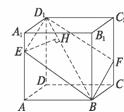
解:由平面与平面平行的性质定理可证BF∥D1E,BE∥D1F.
∴BED1F是平行四边形.作EH⊥BD1于H.
∵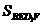 =2·
=2·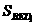 =BD1·EH=EH·
=BD1·EH=EH·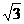 a,
a,
∴要求四边形BED1F面积的最小值,转化为求EH的最小值.
∵AA1∥平面BDD1B1,
∴当且仅当EH为直线AA1到平面BDD1B1的距离时,EH最小,易得EHmin=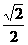 .
.
∴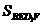 的最小值为
的最小值为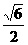 a2.
a2.
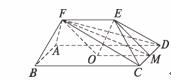
19(2006高考天津卷,理19)如图,在五面体ABCDEF中,点O是矩形ABCD的对角线的交点,面
CDE是等边三角形,棱EF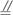
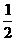 BC.
BC.
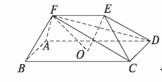
(1)证明FO∥平面CDE;
(2)设BC=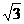 CD,证明EO⊥平面CDF.
CD,证明EO⊥平面CDF.
证明:(1)取CD中点M,连结OM,在矩形ABCD中,
OM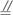
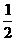 BC,又EF
BC,又EF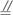
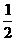 BC,则EF
BC,则EF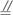 OM.连结EM,
OM.连结EM,
于是四边形EFOM为平行四边形.
∴FO∥EM.
又∵FO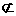 平面CDE,且EM
平面CDE,且EM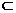 平面CDE,
平面CDE,
∴FO∥平面CDE.
(2)连结FM.由(1)和已知条件,在等边△CDE中,
CM=DM,EM⊥CD且EM=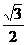 CD=
CD=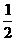 BC=EF.
BC=EF.
因此平行四边形EFOM为菱形,从而EO⊥FM.
∵CD⊥OM,CD⊥EM,
∴CD⊥平面EOM.从而CD⊥EO.
而FM∩CD=M,所以EO⊥平面CDF.
11如下图,点P是一光源,将一投影片放在平面α内,问投影幕所在平面β与平面α______时,投影图象的形状不发生变化.
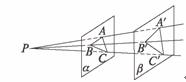
答案:平行
解析:当α∥β时,易证△ABC∽△A′B′C′,从而形状不会发生变化.
12设直线a在平面M内,则平面M平行于平面N是直线a平行于平面N的__________条件.(填“充分不必要”“必要不充分”“充分必要”“既不充分也不?必要?”)
答案:充分不必要
解析:设p:平面M∥平面N,q:直线a∥平面N.
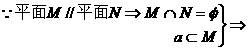 a∩N=
a∩N=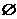
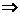 a∥N,?
a∥N,?
∴p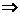 q.
q.
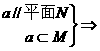 平面N与平面M不一定平行,
平面N与平面M不一定平行,
∴q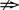 p.
p.
13如图,已知平面α∥平面β,线段AB、CD夹在α、β之间,AB=13,CD=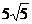 ,且它们在β内的射影之差为2,则α和β之间的距离是____________.
,且它们在β内的射影之差为2,则α和β之间的距离是____________.
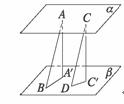
答案:5
解析:设A、C在平面β上的射影为A′、C′,则α、β之间的距离AA′=CC′=a,且BA′、DC′分别为AB、CD在β内的?射影.?
在Rt△ABA′中,AB=13,
则BA′=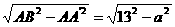 .
.
在Rt△CDC′中,CD=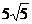 ,
,
则C′D=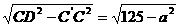 .
.
又∵C′D与A′B相差为2,
即A′B-C′D=2,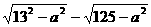 =2.
=2.
∴a=5.∴平面α、β的距离为5.
14设P表示点,m,n,l表示两两不重合的三条直线,以α,β表示两个不重合的平面,那么下列四个命题:①m⊥α,若n⊥α,则m∥n;②m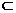 α,n∩α=P,l是n在α内的射影.若m⊥l,则m⊥n;③m⊥α,若n∥a,l∥α,则m⊥n,m⊥l;④m⊥α,若m⊥β,则α∥β中逆命题能成立的序号是________.
α,n∩α=P,l是n在α内的射影.若m⊥l,则m⊥n;③m⊥α,若n∥a,l∥α,则m⊥n,m⊥l;④m⊥α,若m⊥β,则α∥β中逆命题能成立的序号是________.
答案:①②④
解析:命题③的逆命题是:m⊥α,若m⊥n,m⊥l,则n∥α,l∥α,错误的原因在于满足条件的直线n和l可能在平面α内,故①②④能成立.
1设直线l,m,平面α,β,下列条件能得出α∥β的是…( )
A.l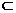 α,m
α,m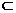 α,且l∥β,m∥β
α,且l∥β,m∥β
B.l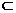 α,m
α,m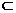 α,且l∥m
α,且l∥m
C.l⊥α,m⊥β,且l∥m
D.l∥α,m∥β,且l∥m
答案:C
解析:
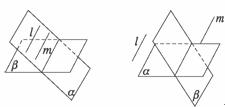
如左上图,A错;如右上图,D错;B显然错.故选C.
2下列命题中正确的是( )
①平行于同一直线的两个平面平行 ②平行于同一平面的两个平面平行 ③垂直于同一直线的两个平面平行 ④与同一直线成等角的两个平面平行
A.①② B.②③ C.③④ D.②③④
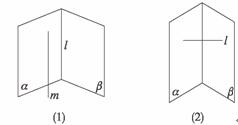
答案:B
解析:如图(1),①错;如图(2),④错.故?选B?.
3给出下列四个命题:①夹在两个平行平面间的线段中,较长的线段与平面所成的角较小;②夹在两个平行平面间的线段相等,则它们与两个平面所成的角相等;③夹在两个平行平面间的线段相等,则这两线段必平行;④夹在两个平行平面间的平行线段必相等.
其中正确的命题有( )
A.①②④ B.②③④ C.①③ D.④
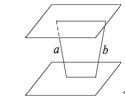
答案:A
解析:由于两个平行平面间的距离是定值,所以①②显然正确;如图,a,b相等,但a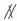 b,故③错;④正确.故选A.
b,故③错;④正确.故选A.
4设α,β表示平面,a表示直线,且直线a不在平面α或β内,并有①α∥β;②a⊥α;③a⊥β.以其中任意两个为条件,另一个为结论,可构造出三个命题.其中正确命题的个数是( )
A.1 B.2 C.3 D.0
答案:C
解析: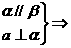 a⊥β,即①②
a⊥β,即①②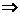 ③.
③.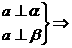 α∥β,即②③
α∥β,即②③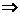 ①.
①.
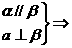 a⊥α,即①③
a⊥α,即①③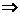 ②.故选C.
②.故选C.
5已知平面α∥平面β,α,β之间的距离等于d,直线a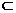 α,则β内?( )
α,则β内?( )
A.有且只有一条直线与a的距离等于d
B.有无数条直线与a的距离等于d
C.所有直线与a的距离都等于d
D.仅有两条直线与a的距离等于d
答案:B
解析:过直线a上任一点作平面β的垂线,垂足为A,过点A在平面β内作直线b∥a,此时a与b间的距离为d;在平面β内所有与a异面的直线间的距离也都是d.
6如果平面α∥平面β,直线a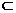 平面α,点B∈β,则平面β内过点B的所有直线中,下列结论成立的是( )
平面α,点B∈β,则平面β内过点B的所有直线中,下列结论成立的是( )
A.不一定存在与a平行的直线
B.不存在与a平行的直线
C.存在唯一一条与a平行的直线
D.存在无数条与a平行的直线
答案:C
解析:如图所示.
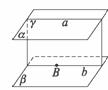
过直线a与点B所确定的平面γ,且γ∩β=b,直线b∥直线a,且唯一.故选C.
7已知m,n是不同的直线,α,β是不重合的平面,给出下列命题:?
①若m∥α,则m平行于平面α内的任意一条直线;
②若α∥β,m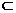 α,n
α,n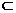 β,则m∥n;
β,则m∥n;
③若m⊥α,n⊥β,m∥n,则α∥β;
④若α∥β,m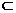 α,则m∥β.
α,则m∥β.
其中正确的命题是( )
A.①②③ B.③④
C.②③ D.④
答案:B
解析:若m∥α,则m平行于过m所作平面与α相交的交线,并非α内任一条直线,故①错;
若α∥β,m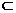 α,n
α,n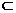 β,则可能m∥n,也可能m,n异面,故②错;
β,则可能m∥n,也可能m,n异面,故②错;
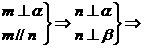 α∥β,③正确;
α∥β,③正确;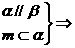 m∥β,④正确.
m∥β,④正确.
8已知平面α∥平面β,C、A∈α,B、D∈β,AB⊥CD,且AB=2,直线AB与平面α所成的角为30°,则线段CD长的取值范围为( )
A.[1,+∞)
B.(1,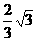 ]
]
C.(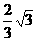 ,
,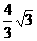 )
D.[
)
D.[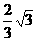 ,+∞)
,+∞)
答案:D
解析:如图,
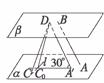
过D作DA′∥AB交平面α于A′,由α∥β,故DA′=AB=2.DA′与α成30°角,由已知DC⊥AB,可得DC⊥DA′,所以DC在过DC且与DA′垂直的平面γ内.令γ∩α=l,在γ内?DC0⊥l时最短,此时DC0=DA′·tan30°=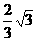 ,故CD≥
,故CD≥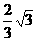 .
.
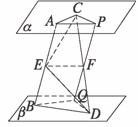
9已知平面α∥平面β,其间夹一垂线段AB=4,另一斜线段CD=6,且AC=BD=3.E、F分别是AB、CD的中点,则EF的长为( )
A.1
B.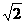 C.2
D.
C.2
D.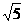
答案:C
解析:如图,过F作AB的平行线,交α、β于P、Q两点,则四边形ABQP为矩形.
∵E、F分别为AB、CD的中点,故EF⊥PQ.
由Rt△EAC≌Rt△EBD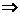 EC=ED,
EC=ED,
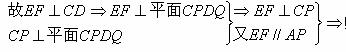 则△APC为直角三角形.
则△APC为直角三角形.
在Rt△CPF中,CP2=CF2-PF2=5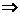 CP=
CP=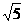 .
.
在Rt△CPA中,AP2=AC2-CP2=32-(.)2=4.
∴AP=2.而AP=EF,∴EF=2.
10一间民房的屋顶有如下图的三种盖法:①单向倾斜;②双向倾斜;③四向倾斜.记三种盖法的屋顶面积分别为P1,P2,P3.若屋顶斜面与水平面所成的角都是α,则( )
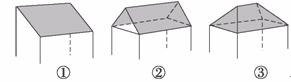
A.P1<P2<P3 B.P1=P2<P3
C.P1<P2=P3 D.P1=P2=P3
答案:D
解析:由S底=S侧cosθ可得P1=P2,
而P3=2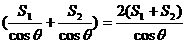
又∵2(S1+S2)=S底,∴P1=P2=P3.
第Ⅱ卷(非选择题)
5.已知正方体ABCD-A1B1C1D1中,求证:平面AB1D1∥平面C1DB.
4.设AB、CD是夹在两个平面a、b之间的异面线段,M、N分别是AB、CD的中点,求证:直线MN∥a.
3.判断题
(1)若一条直线和两个平面成等角,则两个平面平行. ( )
(2)两个平面平行,则一个平面内的任意直线与另一个平面平行. ( )
(3)若直线平行平面,则直线平行平面内的任意直线. ( )
2.填空题
(1)两条直线没有公共点时,它们的位置关系是 ;
两个平面没有公共点时,它们的位置关系是 .
(2)过平面外一点,可以作 条直线与已知平面平行;
过平面外一点,可以作 个平面与已知平面平行.
(3)已知a∥b,它们间的距离为1,直线l与平面a成60°角,则l夹在a、b之间的线段长为 ;
已知a∥b,夹在a、b之间的两条直线所夹部分线段相等,则这两条直线的位置关系是 .
1.选择题
(1)若平面a∥平面b,直线aÌa,直线bÌb,那么直线a,b的位置关系是 ( )
(A)垂直 (B)平行 (C)异面 (D)不相交
(2)当a∥b时,必须满足的条件 ( )
(A)平面a内有无数条直线平行于平面b;
(B)平面a与平面b同平行于一条直线;
(C)平面a内有两条直线平行于平面b;
(D)平面a内有两条相交直线与b平面平行.
4.a,b是异面直线.
(1)求证:过a,b分别有平面a,b,使a∥b.
(2)求证:a,b之间的距离等于a,b之间的距离.
3.已知a∥b,aÌa,bÌb,且a,b是异面直线,A∈a,B∈b,AB=12cm,若AB与b成60°,求a,b之间的距离.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com