
题目列表(包括答案和解析)
1.(1)由已知 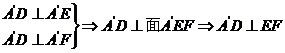 . (4分)
. (4分)
 (2)易知
(2)易知 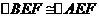
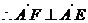 ,又由(1)知
,又由(1)知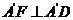 ,
,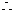
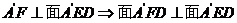 (8分)
(8分)
|
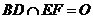 ,易知O为EF中点,且
,易知O为EF中点,且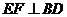
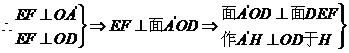
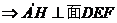
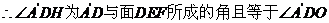
在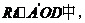 易知
易知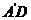 =2,
=2,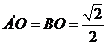 ,
,
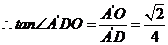 .(14分)
.(14分)
13、
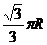 ; 14、 -
; 14、 -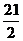 ; 15、2; 16、 ②③ ④.
; 15、2; 16、 ②③ ④.
高二下期数学巩固练习(2)
11、165 12、24
22.(12分)从原点出发的某质点M,按向量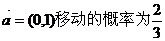 ,按向量
,按向量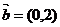 移动的概率为
移动的概率为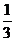 ,设M可到达点(0,n)的概率为Pn.
,设M可到达点(0,n)的概率为Pn.
(1)求P1和P2的值;
(2)求证: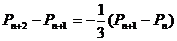 ;
;
21. (12分)杨辉是中国南宋末年的一位杰出的数学家、数学教育家.他的数学著作颇多,他编著的数学书共五种二十一卷,在他的著作中收录了不少现已失传的古代数学著作中的算题和算法.他的数学研究与教育工作的重点是在计算技术方面.杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关.杨辉三角中蕴涵了许多优美的规律.古今中外,许多数学家如贾宪、朱世杰、帕斯卡、华罗庚等都曾深入研究过,并将研究结果应用于其他工作.下面是一个11阶的杨辉三角:
(12分)杨辉是中国南宋末年的一位杰出的数学家、数学教育家.他的数学著作颇多,他编著的数学书共五种二十一卷,在他的著作中收录了不少现已失传的古代数学著作中的算题和算法.他的数学研究与教育工作的重点是在计算技术方面.杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关.杨辉三角中蕴涵了许多优美的规律.古今中外,许多数学家如贾宪、朱世杰、帕斯卡、华罗庚等都曾深入研究过,并将研究结果应用于其他工作.下面是一个11阶的杨辉三角:
试回答:(其中第(1)~(4)小题只须直接给出最后的结果,无须求解过程.)
(1)记第i(i∈N*)行中从左到右的第j(j∈N*)个数为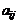 ,则数列{
,则数列{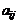 }的通项公式为
;n阶杨辉三角中共有
个数.
}的通项公式为
;n阶杨辉三角中共有
个数.
(2)第k行各数的和是 .
(3)n阶杨辉三角的所有数的和是 .
(4)第p(p∈N*,且p≥2)行除去两端的数字1以外的所有数都能被p整除,则整数p一定为 .
A.奇数 B.质数 C.非偶数 D.合数
(5)在第3斜列中,前5个数依次为1、3、6、10、15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:
第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.
试用含有m、k(m、k∈N*)的数学公式表示上述结论并证明其正确性.
数学公式为: .
证明:
20.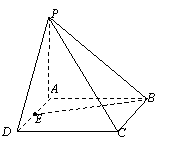 (本小题满分13分)如图,在四棱锥P-ABCD中,底面是矩形且AD=2,
(本小题满分13分)如图,在四棱锥P-ABCD中,底面是矩形且AD=2, 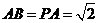 ,PA⊥底面ABCD,E是AD的中点,F在PC上.
,PA⊥底面ABCD,E是AD的中点,F在PC上.
(1)求异面直线PA与EB的距离;
(2)F在何处时,EF⊥平面PBC;
(3)求直线BE与平面PBC所成的角.
19.(13分)袋中有4个白球,6个红球,在抽取这些球的时候谁也无法看到球的颜色.现先由甲取出3个球,并且取出的球将不再放回原袋中,再由乙取出4个球,若规定取得白球多者获胜,试求甲获胜的概率.
18. (本小题满分13分)山坡所在平面
(本小题满分13分)山坡所在平面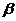 与水平面
与水平面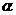 成30°角,坡面上有一条与水平线AB成30°角的直线小路CD,小明沿小路上坡走了200米的路程到达他外婆家(点E),求小明外婆家到水平面的距离.
成30°角,坡面上有一条与水平线AB成30°角的直线小路CD,小明沿小路上坡走了200米的路程到达他外婆家(点E),求小明外婆家到水平面的距离.
17.(13分)投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分,经过多次试验,某生投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋.
(Ⅰ)求该人在4次投掷中恰有三次投入红袋的概率;
(Ⅱ)求该人两次投掷后得2分的概率。
16.已知数列{an},(n∈N*)是首项为a1,公比为q的等比数列,
则a1C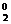 -a2C
-a2C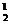 +a3C
+a3C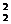 = , a1C
= , a1C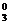 -a2C
-a2C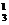 +a3C
+a3C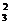 -a4C
-a4C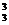 =_______________.
=_______________.
由上述结果归纳概括出关于正整数n的一个结论是________ _________________ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com