
题目列表(包括答案和解析)
2.填空题
(1)三棱锥的三条侧棱两两垂直且长度为1cm、2cm、3cm,则此棱锥的体积为 .
(2)用平行于圆锥底面的平面截圆锥,把圆锥的体积分成相等的两部分,那么截得的小圆锥与原来圆锥的高之比为 .
(3)某长方体的八个顶点中,有四个顶点恰好是一个正四面体的顶点,这个长方体的表面积与正四面体的表面积之比为 .
1.选择题
(1)把一个三棱锥的各棱都增大到原来的2倍,那么它的体积增大的倍数是 ( )
(A)2 (B)4 (C)6 (D)8
(2)侧棱长和底面边长都为1的正三棱锥的体积是 ( )
(A)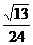 (B)
(B)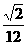 (C)
(C)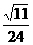 (D)
(D)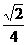
(3)将边长为a的正方形ABCD沿对角线AC折起,使BD=a,则三棱锥D-ABC的体积是 ( )
(A)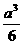 (B)
(B)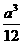 (C)
(C)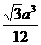 (D)
(D)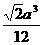
5.棱长为a的正八面体,
(1)求相邻两面所成二面角的大小;
(2)求相邻两面中心间的距离;
(3)求八面体的体积.
4.求正四面体相邻两个面所成二面角的大小
3.将两个棱长相应的正四面体的一个面重合,所得的多面体是正多面体吗?为什么?
2.填空题
(1)已知M={正多面体},N={多面体},R={凸多面体},Q={棱长相等的三棱锥},则集合M、N、R、Q之间的关系是 .
(2)棱长为a的正四面体A-BCD相对两棱AB、CD间的距离是 .
1.选择题
(1)给出下列命题,其中正确的是 ( )
(A)每个面都是正多边形的多面体是正多边形
(B)每个面都是相同边数正多边形的多面体是正多边形
(C)长方体的各侧面是正方形时,它就是正多边形
(D)正三棱锥是正四面体.
(2)下列命题中假命题的是 ( )
(A)多面体的面数最少是4个 (B)正多面体有且只有五种
(C)四面体都是三棱锥 (D)五面体就是三棱柱
25、解:(1)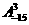 =(-15)(-16)(-17)=4080; (3分)
=(-15)(-16)(-17)=4080; (3分)
(2)性质①、②均可推广,推广的形式分别是
①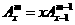 ,②
,②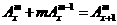 (x∈R,m∈N+)
(x∈R,m∈N+)
事实上,在①中,当m=1时,左边=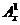 =x,右边=x
=x,右边=x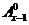 =x,等式成立; (4分)
=x,等式成立; (4分)
当m≥2时,左边=x(x-1)(x-2)…(x-m+1)=x{(x-1)(x-2)…[(x-1)-(m-1)+1]}=x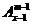 ,
,
因此,①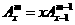 成立; (5分)
成立; (5分)
在②中,当m=l时,左边=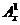 +
+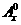 =x+l=
=x+l=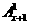 =右边,等式成立;
=右边,等式成立;
当m≥2时,左边=x(x-1)(x-2)…(x-m+1)+mx(x-1)(x-2)…(x-n+2)
=x(x-1)(x-2)…(x-m+2)[(x-m+1)+m]
=(x+1)x(x-1)(x-2)…[(x+1)-m+1]=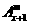 =右边,
(6分)
=右边,
(6分)
因此②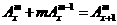 (x∈R,m∈N+)成立.
(8分)
(x∈R,m∈N+)成立.
(8分)
(3)先求导数,得( )/=3x2-6x+2.令3x2-6x+2>0,解得x<
)/=3x2-6x+2.令3x2-6x+2>0,解得x<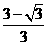 或x>
或x>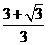
因此,当x∈(-∞,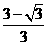 )时,函数为增函数,当x∈(
)时,函数为增函数,当x∈(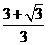 ,+∞)时,函数也为增函数. (11分)
,+∞)时,函数也为增函数. (11分)
令3x2-6x+2≤0, 解得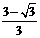 ≤x≤
≤x≤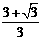 ,因此,当x∈[
,因此,当x∈[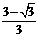 ,
,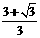 ]时,函数为减函数.
(12分)
]时,函数为减函数.
(12分)
∴函数 的增区间为(-∞,
的增区间为(-∞,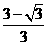 ),(
),(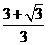 ,+∞);减区间为[
,+∞);减区间为[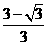 ,
,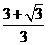 ].
].
24、解:(1)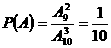 ; (2)
; (2) 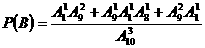 。
。
23、解:设A={甲中彩} B={乙中彩} C={甲、乙都中彩} 则C=AB
(1)P(A)=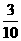 ;(2)P(C)=P(AB)=
;(2)P(C)=P(AB)=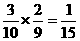
(2)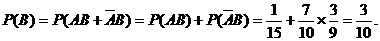
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com