
题目列表(包括答案和解析)
6. 如果某物体做运动方程为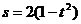 的直线运动(s的单位为m,t的单位为s),那么其在1.2s末的瞬时速度为( )
的直线运动(s的单位为m,t的单位为s),那么其在1.2s末的瞬时速度为( )
A. -0.88m/s B. 0.88 m/s C. -4.8 m/s D.4.8 m/s
7 曲线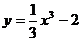 在点(
在点(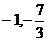 )处切线的倾斜角为( )
)处切线的倾斜角为( )
A.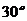 B.
B. 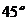 C.
C.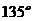 D.
D.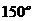
8 函数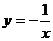 在点(
在点(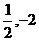 )处的切线方程为( )
)处的切线方程为( )
A.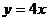 B.
B.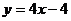 C.
C.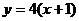 D.
D.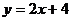
二 填空题
5. 已知曲线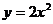 上一点A(2,8),则A处的切线斜率为( )
上一点A(2,8),则A处的切线斜率为( )
A. 4 B.16 C.8 D. 2
4. 一质点运动的方程为 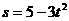 ,则在一段时间
,则在一段时间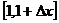 内相应的平均速度为( )
内相应的平均速度为( )
A.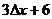 B.
B.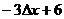 C.
C.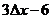 D.
D.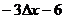
3. 在曲线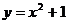 的图像上取一点(1,2),及附近一点(
的图像上取一点(1,2),及附近一点(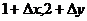 ),则
),则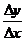 为( )
为( )
A.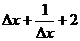 B.
B.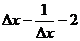 C.
C.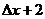 D.
D.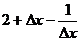
1 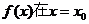 处存在导数,则
处存在导数,则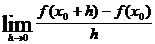 ( )
( )
A.与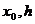 都有关
B.仅与
都有关
B.仅与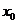 有关,而与
有关,而与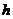 无关
无关
C.仅与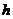 有关而与
有关而与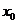 无关 D.与
无关 D.与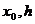 都无关
都无关
2. 某质点沿直线运动的方程为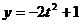 ,则该质点从
,则该质点从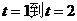 时的平均速度为( )
时的平均速度为( )
A. -4 B.-8 C.6 D.-6
如果直线l是过P和Q的公切线,则①式和②式都是l的方程,
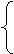 x1+1=-x2
x1+1=-x2
所以
- x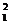 =x
=x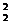 +a.
+a.
消去x2得方程 2x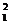 +2x2+1+a=0.
+2x2+1+a=0.
若判别式△=4-4×2(1+a)=0时,即a=-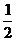 时解得x1=-
时解得x1=-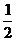 ,此时点P与Q重合.
,此时点P与Q重合.
即当a=-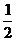 时C1和C2有且仅有一条公切线,由①得公切线方程为 y=x-
时C1和C2有且仅有一条公切线,由①得公切线方程为 y=x-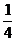 .
.
(Ⅱ)证明:由(Ⅰ)可知.当a<-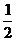 时C1和C2有两条公切线
时C1和C2有两条公切线
设一条公切线上切点为:P(x1,y1), Q(x2 , y2 ).
其中P在C1上,Q在C2上,则有
x1+x2=-1,
y1+y2=x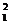 +2x1+(-x
+2x1+(-x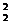 +a)= x
+a)= x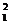 +2x1-(x1+1)2+a=-1+a .
+2x1-(x1+1)2+a=-1+a .
线段PQ的中点为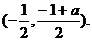
同理,另一条公切线段P′Q′的中点也是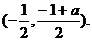
所以公切线段PQ和P′Q′互相平分.
讲评:本小题主要考查导数、切线等知识及综合运用数学知识解决问题的能力
函数y=-x2+a的导数y′=-2x, 曲线C2 在点Q(x2,-x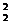 +a)的切线方程是
+a)的切线方程是
4.用以上结论证明空间四边形对边是异面直线.
3.命题“平面内一点和平面外一点的连线和平面内不过该点的直线是异面直线”
(1)改写为符号叙述
(2)试证明该命题.
2.画图表示两条异面直线(至少要画两种不同的图形)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com