1．选择题

　(1)已知a∥平面a，bÌa，那么a，b的位置关系是　　　　　　　　　　　　　　　　　　 (　 )

　　　　 (A)a∥b　　　　　　　　　　　　　　　　　　　　　　　　 (B)a，b异面　　　　

　　　　 (C)a∥b或a，b异面　　　　　　　　　　　　　　 (D)a∥b或a⊥b

　(2)如果直线l与一平面平行，夹在直线和平面间的两条线段长相等，那么这两条线段所在直线的位置关系是　　　　　　 　　　　　　　　　　　　　　 (　 )

　　　　 (A)平行　　　　　　　 (B)相交　　　　　　　　 (C)异面　　　　　　 (D)以上都有可能

　(3)下列命题中正确的是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

　　　　 (A)如果两条直线没有公共点，那么这两条直线平行；

　　　　 (B)如果两条直线都和第三条直线平行，那么这两条直线平行；

　　　　 (C)如果两条直线都平行于同一个平面，那么这两条直线平行；

　　　　 (D)如果两条直线都和第三条直线垂直，那么这两条直线平行.

　(4)平面外两条异面直线在平面内的射影是　　　　　　　　　　　　　　　　　　　　　 (　 )

　　　　 (A)两条相交直线　　　　　　　　　　　　　　　　　 (B)两条平行直线

　　　　 (C)一条直线和一个点　　　　　　　　　　　　　 (D)以上都有可能

　(5)a，b是两条异面直线，下面结论正确的是　　　　　　　　　　　　　　　　　　　 (　 )

　　　　 (A)过不在a，b上任意一点，可以作一个平面与a，b都平行；

　　　　 (B)过不在a，b上任意一点，可以作一条直线与a，b都相交；

　　　　 (C)过不在a，b上任意一点，可以作一条直线与a，b都平行；

　　　　 (D)过a可以并且只可以作一个平面与b平行.

　(6)PA垂直于以AB为直径的圆所在的平面，C为圆周上除A、B外的任意一点，则下列结论中不成立的是　　　　 　　　　　　　　　　　　　　 (　 )

　　　　 (A)PC⊥CB　　　　　　　　　　　　　　　　　　　　　 (B)BC⊥平面PAC

　　　　 (C)AC⊥PB　　　　　　　　　　　　　　　　　　　　　 (D)PB与平面PAC的夹角是∠BPC

　(7)已知平面a的斜线l与a所成的角为θ，在平面a内任意引l的异面直线m，则l与m所成的角有　　　　　　　　　　 　　　　　　　　　　　　　　 (　 )　　　　　　　　　　

　　　　 (A)最小值是θ，最大值是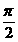　　　　　　　　 (B)最小值是θ，最大值是π-θ

　　　　 (C)最小值是θ，最大值是π　　　　　　　　 (D)不存在最小值与最大值.

　(8)一条线段AB的两端点A，B和平面a的距离分别是30cm和50cm，P为AB上一点，且PA∶PB=3∶7，则P到平面a的距离为　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

　　　　 (A)36cm　　　　　　　 (B)6cm　　　　　　　　　 (C)36cm或6cm　　　 (D)以上都不对

　(9)在正方体ABCD-A₁B₁C₁D₁中，E、F分别是底面上AB、BC的中点，M为EF的中点，则B₁M与面ABCD的夹角θ满足　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

　　　　 (A)tgθ=2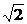　　 (B)tgθ=　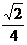　　　 (C)coSθ=　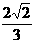　 (D)θ=60º

(10)以下四个命题中，不正确的有几个　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

①　　 直线a，b与平面a成等角，则a∥b；

②　　 两直线a∥b，直线a∥平面a，则必有b∥平面a；

③　　 一直线与平面的一斜线在平面a内的射影垂直，则必与斜线垂直；

④　　 两点A，B与平面a的距离相等，则直线AB∥平面a

　　　　 (A)0个　　　　　　　　 (B)1个　　　　　　　　　 (C)2个　　　　　　　　　 (D)3个

12．两个边长为2的正方形ABCD和ADEF各与对方所在平面垂直，M、N分别是对角线AE、BD上的点，且EM=DN

　(1)求证：MN∥平面DCE；

　(2)设EM=x，MN=y，求y与x的函数关系式；

　(3)求M、N两点间的最短距离.

11．⊿ABC中，AB=3，BC=4，B=45°，且BC边在平面a内，⊿ABC所在平面a成30°角，求⊿ABC在平面a内的射影的面积.

10．在空间四边形ABCD中，AB=BC=CD=DA=BD=AC=a，E、F为BD、AD的中点，求证：EF是BC与AD的公垂线，并求EF的长.

9．a、b是两个不同的平面，m、n是平面a及b之外的两条不同直线，给出四个论断：①m⊥n；

②a⊥b；

③n⊥b；

④m⊥a

以其中三个论断作为条件，余下一个论断作为结论，写出你认为正确的一个命题　　　　　　　　　　　　　　　　　　　　　　　 .

8．点A是二面角a-l-b内一点，AB⊥a于B，AC⊥b于C，设AB=3，AC=2，∠BAC=60°，则点A到棱l的距离是　　　　　　　　　 .

7．直角三角形ABC的斜边BC在平面a内，顶点AÏa，则⊿ABC的两条直角边在平面a内的射影与斜边BC所成的图形是　 　　　　　　　.

6．若两条异面直线所成的角为80°，则过空间任意一点P的直线与这两条直线所成的角都是50°，这样的直线有且仅有　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

　　　　 (A)1条 　　　　　　　 (B)2条 　　　　　　　　 (C)3条 　　　　　　　　 (D)4条

5．a、b是两个不重合的平面，在下列条件中可判定a∥b的是　　　　　　　　　　　 (　 )

　　　　 (A)a、b都垂直于平面g

　　　　 (B)a内不共线的三点到b的距离相等

　　　　 (C)l、m是a内两直线，且l∥b，m∥b

　　　　 (D)l、m是两条异面直线，且l∥a，m∥a，l∥b，m∥b

4．从平面外一点向平面引垂线和若干斜线，若斜线和平面所成的角相等，则(　 )

　　　　 (A)斜足是一个正多边形的顶点 　　　　　 (B)垂足是斜足多边形内切圆的圆心 　　　 (C)垂足是斜足多边形外接圆的圆心 　　　　　　　　　　　　　　 (D)垂足是斜足多边形的垂心