
题目列表(包括答案和解析)
3、在△ABC中,根据下列条件解三角形,其中有一解的是 ( )
A.b=7,c=3,C=30° B.b=5,c=4 ,B=45°
C.a=6,b=6 ,B=60° D.a=20,b=30,A=30°
1、已知△ABC中,a=4,b=4 ,∠A=30°,则∠B等于 (
)
A.30° B.30°或150° C.60° D.60°或120°
2、已知△ABC中,AB=6,∠A=30°,∠B=120°,则△ABC的面积( )
A.9 B.18 C.9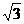 D.18
D.18
20.解:⑴∵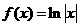 ,
,
∴当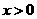 时,
时,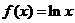 ; 当
; 当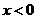 时,
时,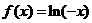
∴当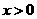 时,
时,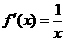 ; 当
; 当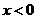 时,
时,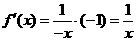 .
.
∴当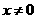 时,函数
时,函数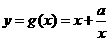 .
.
⑵∵由⑴知当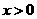 时,
时,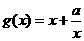 ,
,
∴当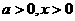 时,
时, 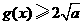 当且仅当
当且仅当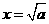 时取等号.
时取等号.
∴函数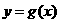 在
在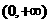 上的最小值是
上的最小值是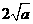 ,∴依题意得
,∴依题意得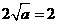 ∴
∴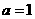 .
.
⑶由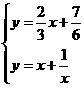 解得
解得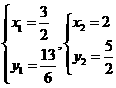
∴直线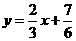 与函数
与函数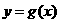 的图象所围成图形的面积
的图象所围成图形的面积
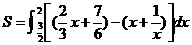 =
=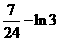
19.证明:∵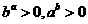 ∴要证:
∴要证: 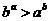
只要证: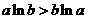
只要证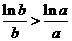 .(∵
.(∵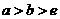 )
)
取函数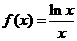 ,∵
,∵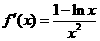
∴当 时,
时,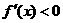 ,∴函数
,∴函数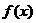 在
在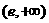 上是单调递减.
上是单调递减.
∴当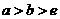 时,有
时,有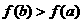 即
即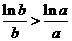 .得证
.得证
18.(1) 证: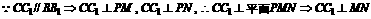 ;
;
(2) 解:在斜三棱柱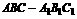 中,有
中,有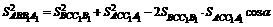 ,其中
,其中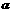 为
为
平面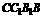 与平面
与平面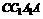 所组成的二面角.
所组成的二面角.
 上述的二面角为
上述的二面角为 ,在
,在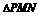 中,
中,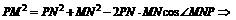
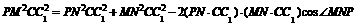 ,
,
由于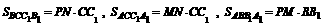 ,
,
∴有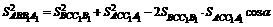 .
.
17.解: 答f(x)在[-4,4]上是单调递减函数.
证明:∵函数f(x)的图象关于原点成中心对称,
则f(x)是奇函数,所以a=1,b=0,于是f(x)=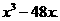
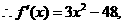 ∴当
∴当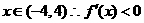
又∵函数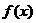 在
在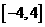 上连续
上连续
所以f(x)在[-4,4]上是单调递减函数.
16.解:⑴由y=x3+x-2,得y′=3x2+1,
由已知得3x2+1=4,解之得x=±1.当x=1时,y=0;当x=-1时,y=-4.
又∵点P0在第三象限,
∴切点P0的坐标为 (-1,-4).
⑵∵直线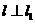 ,
,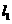 的斜率为4,∴直线l的斜率为
的斜率为4,∴直线l的斜率为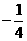 ,
,
∵l过切点P0,点P0的坐标为 (-1,-4)
∴直线l的方程为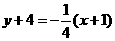 即
即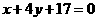 .
.
15.解:∵当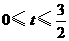 时,
时,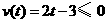 ; 当
; 当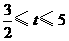 时,
时,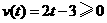 .
.
∴物体从时刻t=0秒至时刻 t=5秒间运动的路程
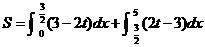 =
=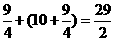 (米)
(米)
13.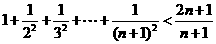 (n∈N*)
14.二
(n∈N*)
14.二
12.夹在两个平行平面间的平行线段相等;真命题.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com