
(17)(本小题满分12分)
已知数列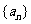 是首项
是首项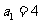 、公比
、公比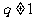 的等比数列,
的等比数列,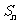 是其前n项的和,且
是其前n项的和,且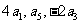 成等差数列.
成等差数列.
(I)求公比q的值;
(II)设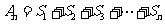 ,求
,求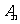 .
.
(18)(本小题满分12分)
已知函数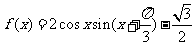 .
.
(I)求函数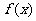 的最小正周期T;
的最小正周期T;
(Ⅱ)若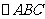 的三边a,b,c 满足
的三边a,b,c 满足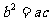 ,且边b所对的角为B,试求cosB的取值范围,并确定此时
,且边b所对的角为B,试求cosB的取值范围,并确定此时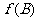 的最大值.
的最大值.
(19)(本小题满分12分)
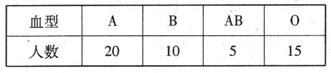 某高等学校自愿献血的50位同学的血型分布情形如下表:
某高等学校自愿献血的50位同学的血型分布情形如下表:
(I)今从这50人中随机选出两人,问两人血型相同的概率是多少?
(Ⅱ)今有A血型的病人需要输血,从血型为A、O的同学中随机选出2人准备献血,记选出A血型的人数为 ,求随机变量
,求随机变量 的分布列及数学期望E
的分布列及数学期望E .
.
(20)(本小题满分12分)
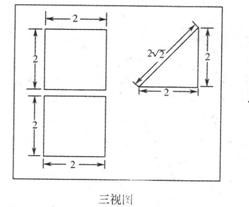 一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点).
一个多面体的直观图及三视图如图所示:(其中M、N分别是AF、BC的中点).
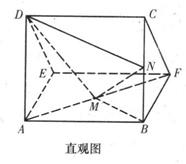
(I)求证:MN∥平面CDEF;
(Ⅱ)求二面角D-MN-B的余弦值的绝对值.
(21)(本小题满分12分)
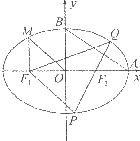
如图,已知A、B、C是椭圆 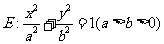 上的三点,其中点A的坐标为(
上的三点,其中点A的坐标为(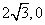 ) ,BC过椭圆的中心O,且
) ,BC过椭圆的中心O,且 .
.
(I)求点C的坐标及椭圆E的方程;
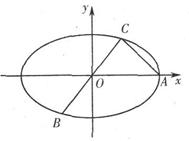 (Ⅱ)若椭圆E上存在两点P、Q,使得
(Ⅱ)若椭圆E上存在两点P、Q,使得 的平分线总是垂直于x轴,试判断向量
的平分线总是垂直于x轴,试判断向量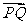 与
与 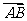 是否共线,并给出证明.
是否共线,并给出证明.
(22)(本小题满分14分)
已知函数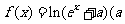 为常数,e为自然对数的底数)是实数集R上的奇函数,函数
为常数,e为自然对数的底数)是实数集R上的奇函数,函数
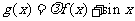 是区间[-1,1]上的减函数.
是区间[-1,1]上的减函数.
(I)求a的值;
(Ⅱ)若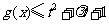 在
在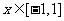 上恒成立,求t的取值范围;
上恒成立,求t的取值范围;
(Ⅲ)讨论关于x的方程 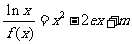 的根的个数.
的根的个数.
(13)已知二项式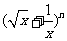 的展开式的第6项为常数项,则n=
.
的展开式的第6项为常数项,则n=
.
(14)在Rt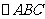 中,
中,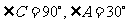 ,则以A、B为焦点,过点C的椭圆的离心率是
.
,则以A、B为焦点,过点C的椭圆的离心率是
.
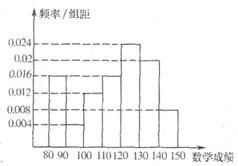 (15)某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试
(15)某地教育部门为了了解学生在数学答卷中的有关信息,从上次考试
的10000名考生的数学试卷中,用分层抽样的方法抽取500人,并
根据这500人的数学成绩画出样本的频率分布直方图(如图),则这
10000人中数学成绩在[140,150]段的约是 人.
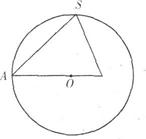 (16)已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱 锥及球面所得截面如右图,则此三棱锥的侧面积为
. (注:底面是正三角形,且顶点在底面上的射影是底面中心的三棱锥,叫做正三棱锥.)
(16)已知正三棱锥S-ABC内接于半径为6的球,过侧棱SA及球心O的平面截三棱 锥及球面所得截面如右图,则此三棱锥的侧面积为
. (注:底面是正三角形,且顶点在底面上的射影是底面中心的三棱锥,叫做正三棱锥.)
(1)复数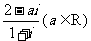 是纯虚数,则a =
是纯虚数,则a =
(A)0 (B)1 (C)2 (D)3
(2)抛物线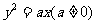 的焦点到其准线的距离是
的焦点到其准线的距离是
(A)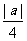 (B)
(B)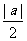 (C)
(C)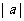 (D)
(D)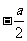
(3)用二分法研究函数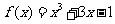 的零点时,第一次经计算
的零点时,第一次经计算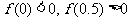 ,可得其中一个零点
,可得其中一个零点
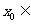 ,第二次应计算
.以上横线上应填的内容为
,第二次应计算
.以上横线上应填的内容为
(A)(0,0.5),f (0.25) (B)(0,1),f (0.25)
(C)(0.5,1),f (0.75) (D)(0,0.5),f (0.125)
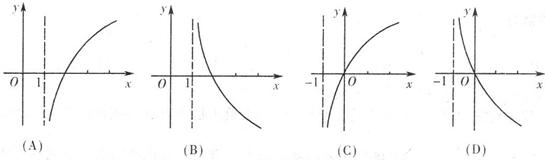 (4)若函数
(4)若函数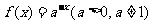 是定义域为R的增函数,则函数
是定义域为R的增函数,则函数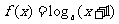 的图象大致是
的图象大致是
(5)已知a、b 表示直线,α 、β表示平面,则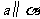 的一个充分条件是
的一个充分条件是
(A)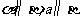 (B)
(B)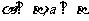
(C)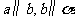 (D)
(D)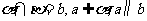
(6)过抛物线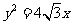 的焦点,且与圆
的焦点,且与圆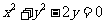 相切的直线方程是
相切的直线方程是
(A)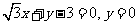 (B)
(B)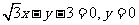
(C)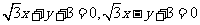 (D)
(D)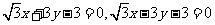
(7)已知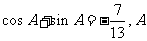 为第四象限角,则
为第四象限角,则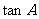 等于
等于
(A)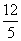 (B)
(B)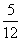 (C)
(C)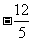 (D)
(D)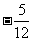
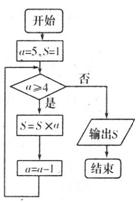 (8)右面的程序框图输出的结果是
(8)右面的程序框图输出的结果是
(A)5
(B)10
(C)15
(D)20
(9)已知函数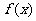 是以2为周期的偶函数,且当
是以2为周期的偶函数,且当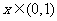 时,
时,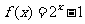 ,则
,则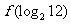 的值为
的值为
(A)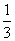 (B)
(B)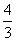 (C)2
(D)11
(C)2
(D)11
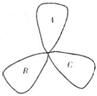 (10)荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如下图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是
(10)荷花池中,有一只青蛙在成品字形的三片荷叶上跳来跳去(每次跳跃时,均从一叶跳到另一叶),而且逆时针方向跳的概率是顺时针方向跳的概率的两倍,如下图.假设现在青蛙在A叶上,则跳三次之后停在A叶上的概率是
(A)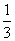 (B)
(B)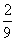 (C)
(C)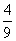 (D)
(D)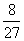
(11)已知等差数列{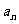 }的前n项和为
}的前n项和为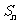 ,若
,若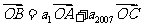 ,且A、B、C三点共线(O为该直线外一点),则
,且A、B、C三点共线(O为该直线外一点),则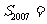
(A)2007
(B)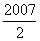 (C)
(C)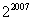 (D)
(D)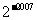
(12)点P是双曲线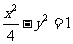 的右支上一点,M、N分别是
的右支上一点,M、N分别是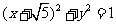 和
和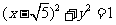 上的点,则
上的点,则 的最大值是
的最大值是
(A)2 (B)4 (C)6 (D)8
第Ⅱ卷 (非选择题 共90分)
22.(本小题满分14分)
设函数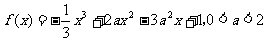 .
.
(1)求函数 的单调区间、极值;
的单调区间、极值;
(2)若当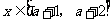 时,恒有
时,恒有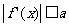 ,试确定
,试确定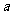 的取值范围.
的取值范围.
21.(本小题满分12分)
已知数列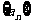 的前
的前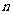 项和
项和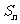 ,且
,且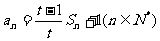 ,其中t为正常数,且
,其中t为正常数,且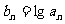
(1)求数列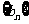 的通项公式;
的通项公式;
(2)当t≠1 时,设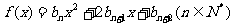 的图像在
的图像在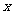 轴上截得的线段长为
轴上截得的线段长为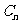 ,求
,求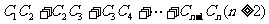 .
.
20.(本小题满分12分)
如图所示,从椭圆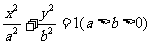 上一点
上一点 向
向 轴作垂线,恰好通过椭圆的左焦点
轴作垂线,恰好通过椭圆的左焦点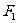 ,且它的长轴端点A及短轴的端点B的连线
,且它的长轴端点A及短轴的端点B的连线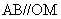 .
.
(1)求椭圆的离心率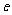 ;
;
(2)设Q是椭圆上一点,当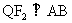 时,延长
时,延长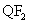 与椭圆交于另一点
与椭圆交于另一点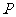 ,若
,若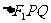 的面积为
的面积为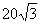 ,求此时椭圆的方程.
,求此时椭圆的方程.
19.(本小题满分12分)
某商场预计全年分批购入每台价值为2000元的电视机共3600台,每批都购入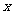 台(
台(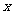 是正整数),且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比,若每批购入400台,则全年需用去运费和保管费共43600元,现在全年只有24000元资金可以用于支付这笔费用,请问:能否恰当地安排每批进货的数量,使
是正整数),且每批均需付运费400元,储存购入的电视机全年所付保管费与每批购入电视机的总价值(不含运费)成正比,若每批购入400台,则全年需用去运费和保管费共43600元,现在全年只有24000元资金可以用于支付这笔费用,请问:能否恰当地安排每批进货的数量,使
资金够用?写出你的结论,并说明理由.
18.(本小题满分12分)
已知直四棱柱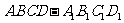 的底面是菱形,
的底面是菱形,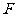 为
棱
为
棱 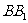 的中点,
的中点, 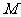 为线段
为线段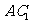 的中点.
的中点.
(1)求证:直线MF//平面ABCD:
(2)求证:平面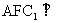 平面
平面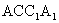
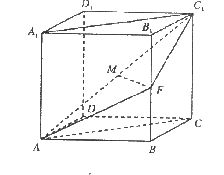
17.(本小题满分12分)
已知向量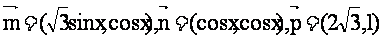
(1)若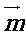 ∥
∥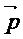 ,求
,求 的值;
的值;
(2)若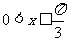 ,求函数
,求函数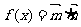 的值域.
的值域.
16.下列命题中,真命题的序号有_______(写出所有真命题的序号).
①直线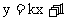 与椭圆
与椭圆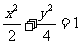 总有两个交点;
总有两个交点;
②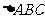 中,
中,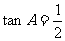 ,
,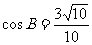 ,则此三角形的最大角为
,则此三角形的最大角为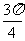 ;
;
③已知:a、b、c∈R 且 c<b<a,ac<0 则 ab<ac;
③过原点且与曲线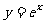 相切的切线方程为
相切的切线方程为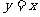 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com