（Ⅱ）证明曲线C与C₁关于点A（）对称；

86.（1998全国理，24）设曲线C的方程是y=x³－x，将C沿x轴、y轴正向分别平行移动t、s单位长度后得曲线C₁.

（Ⅰ）写出曲线C₁的方程；

85.（1999上海，22）设椭圆C₁的方程为=1（a＞b＞0），曲线C₂的方程为y=，且C₁与C₂在第一象限内只有一个公共点P.

（Ⅰ）试用a表示点P的坐标.

（Ⅱ）设A、B是椭圆C₁的两个焦点，当a变化时，求△ABP的面积函数S（a）的值域；

（Ⅲ）设min｛y₁，y₂，…，y_n｝为y₁，y₂，…，y_n中最小的一个.设g（a）是以椭圆C₁的半焦距为边长的正方形的面积，求函数f（a）=min｛g（a），S（a）｝的表达式.

84.（1999全国，24）如图8―8，给出定点A（a，0）（a＞0）和直线l：x=－1.B是直线l上的动点，∠BOA的角平分线交AB于点C.求点C的轨迹方程，并讨论方程表示的曲线类型与a值的关系.

注：文科题设还有条件a≠1

83.（2000上海，17）已知椭圆C的焦点分别为F₁（，0）和F₂（2，0），长轴长为6，设直线y=x+2交椭圆C于A、B两点，求线段AB的中点坐标．

82.（2000全国文，22）如图8―7，已知梯形ABCD中|AB|＝2|CD|，点E分有向线段所成的比为，双曲线过C、D、E三点，且以A、B为焦点．求双曲线离心率．

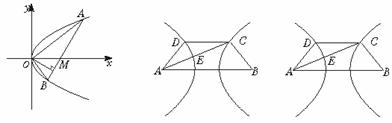
图8―5              图8―6            图8―7

81.（2000全国理，22）如图8―6，已知梯形ABCD中，|AB|＝2|CＤ|，点E分有向线段所成的比为λ，双曲线过C、D、E三点，且以A、B为焦点．当≤λ≤时，求双曲线离心率e的取值范围．

80.（2000京皖春，23）如图8―5，设点A和B为抛物线y²＝4px（p＞0）上原点以外的两个动点，已知OA⊥OB，OM⊥AB，求点M的轨迹方程，并说明它表示什么曲线．

79.（2000上海春，22）如图8―4所示，A、F分别是椭圆＝1的一个顶点与一个焦点，位于x轴的正半轴上的动点T（t，0）与F的连线交射影OA于Q．求：

（1）点A、F的坐标及直线TQ的方程；

（2）△OTQ的面积S与t的函数关系式S=f（t）及其函数的最小值；

（3）写出S=f（t）的单调递增区间，并证明之．