所以M（，0），N（，0）

87.解法一：如图8―24建立坐标系，以l₁为x轴，MN的垂直平分线为y轴，点O为坐标原点.

依题意知：曲线段C是以点N为焦点，以l₂为准线的抛物线的一段，其中A、B分别为C的端点.

设曲线段C的方程为

y²=2px（p＞0），（x_A≤x≤x_B，y＞0）

其中x_A、x_B分别为A、B的横坐标，p＝|MN|．

即，∴s＝－t且t≠0.

评述：本小题主要考查函数图象、方程与曲线，曲线的平移、对称和相交等基础知识，考查运动、变换等数学思想方法，以及综合运用数学知识解决问题的能力.

所以方程组有且仅有一组解

消去y整理得3tx²－3t²x＋（t³－t－s）＝0

这个关于x的一元二次方程有且仅有一个根.

所以t≠0并且其根的判别式Δ＝9t⁴－12t（t³－t－s）＝0

是B₁关于点A的对称点，则有．

所以x₁＝t－x₂，y₁＝s－y₂．

代入曲线C的方程，得x₂和y₂满足方程：s－y₂＝（t－x₂）³－（t－x₂），

即y₂＝（x₂－t）³－（x₂－t）＋s

可知点B₂（x₂，y₂）在曲线C₁上.

反过来，同样可以证明，在曲线C₁上的点关于点A的对称点在曲线C上，因此，曲线C与C₁关于点A对称.

（Ⅲ）证明：因为曲线C与C₁有且仅有一个公共点

86.（Ⅰ）解：曲线C₁的方程为y＝（x－t）³－（x－t）＋s．

（Ⅱ）证明：在曲线C上任取一点B₁（x₁，y₁），设B₂（x₂，y₂）

故f（a）=min｛g（a），S（a）｝=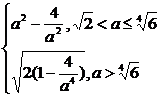

解得：a≤（舍去）或a≥，

即a²－≥，

整理得：a⁸－10a⁴+24≥0，

即（a⁴－4）（a⁴－6）≥0，

即（a⁴－4）（a⁴－6）≥0

（Ⅲ）解：g（a）=c²=a²－b²=a²－，

解不等式：g（a）≥S（a），