
题目列表(包括答案和解析)
1、从点P出发引三条射线PA、PB、PC,每两条的夹角都是60°,则二面角B-PA-C的余弦值是 ( )
A.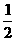 B.
B.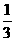 C.
C.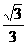 D.
D.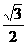
3、求二面角大小时一般按“一作,二证,三计算”步骤进行.
重点难点
重点是在具体问题中如何作出平面角,并能求出该角,比较困难的是求没有给出的棱的二面角大小.
基础练习
2、二面角的平面角的三种作法;
1、二面角,二面角的平面角的定义;
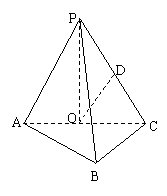
8、如右图,在三棱锥P-ABC中,AB⊥BC,AB=BC=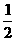 PA,点O、D分别是AC、PC的中点,OP⊥底面ABC, (1)求证:OD∥平面PAB;
PA,点O、D分别是AC、PC的中点,OP⊥底面ABC, (1)求证:OD∥平面PAB;
(2)求直线OD与平面PBC所成角的大小.
高三数学教学案 第九章 立体几何
第十一课时 二面角(一)
考纲摘录
掌握平面与平面所成角的概念,能正确画出两个平面位置关系的图形,并能运用二面
角及其平面角的概念进行计算和证明.
知识概要
7、在三棱柱ABC-A1B1C1中,四边形A1ABB1是菱形,四边形BCC1B1是矩形,
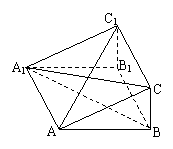 C1B1⊥AB.(1)求证:平面CA1B⊥A1AB;(2)若C1B1=3,AB=4,∠ABB1=60°,求AC1与平面BCC1所成角的大小.
C1B1⊥AB.(1)求证:平面CA1B⊥A1AB;(2)若C1B1=3,AB=4,∠ABB1=60°,求AC1与平面BCC1所成角的大小.
7、已知∠BOC在平面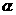 内,OA是
内,OA是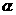 的斜线,若∠AOB=AOC=60°,OB=OC=
的斜线,若∠AOB=AOC=60°,OB=OC=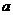 ,BC=
,BC=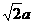 ,求OA和平面
,求OA和平面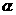 所成的角.
所成的角.
6、已知平面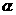 与
与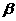 所成的二面角为80°,P为
所成的二面角为80°,P为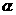 、
、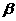 外一定点,过点P的一条直线与
外一定点,过点P的一条直线与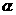 、
、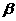 所成的角为30°,则这样的直线有且仅有( )
所成的角为30°,则这样的直线有且仅有( )
A.1条 B.2条 C.3条 D.4条
5、在正四面体ABCD中,E为棱AD中点,则CE与平面BCD所成角的正弦值为__________.
4、平面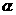 的斜线与
的斜线与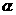 所成的角为30°,则此斜线和
所成的角为30°,则此斜线和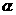 内所有不过斜足的直线所成角的最大值是( )
内所有不过斜足的直线所成角的最大值是( )
A.30° B.60° C.90° D.150°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com