
题目列表(包括答案和解析)
7.已知正六棱锥的侧面与底面所成的角为α,侧棱与底面所成的角为β,则tanβ·cotα的值为 ( )
A.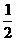 B.
B.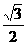 C.
C.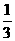 D.
D.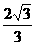
联想:(1)已知三棱锥P-ABC中,∠APB=∠BPC=∠CPA=900三棱锥侧面与底面所成的角分别为α1,α2,α3,则下列各式中正确的是 ( )
A.sinα1sinα2sinα3=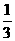 B.sin2α1+sin2α2+sin2α3=1
B.sin2α1+sin2α2+sin2α3=1
C.cosα1cosα2cosα3=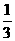 D.cos2α1+cos2α2+cos2α3=1
D.cos2α1+cos2α2+cos2α3=1
(2)正三棱锥的侧棱长是底面边长的k倍,则k的取值范围是 ( )
A.(0,+∞) B.(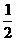 ,+∞) C.(
,+∞) C.(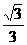 ,+∞) D.[
,+∞) D.[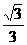 ,+∞]
,+∞]
(3)正四棱锥P-ABCD的棱长均为a,点E是分PA为1:2的内分点,F和G分别是分EB和ED的比为2:1的内分点,则异面直线PC和FG所成角是 ( )
A.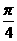 B.
B.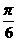 C.
C.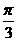 D.
D.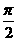
(4)正方体AC1中,E,F分别为棱AB,C1D1的中点,则A1B1与截面A1ECF所成角的正弦值为 。
(5)在正方体ABCD-A1B1C1D1中,M是棱DD1的中点,O为底面ABCD的中心,P为棱A1B1上任意一点,则直线OP与直线AM所成的角为 ( )
A.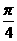 B.
B.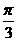 C.
C.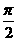 D.不确定
D.不确定
6.给出4个命题:
①到两定点距离之和为常数的动点的轨迹是椭圆;
②到两个定点的距离之差的绝对值为常数的点的轨迹是双曲线;
③到定直线x=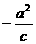 和定点F(-c,0)的距离之比为
和定点F(-c,0)的距离之比为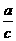 (c > a >0)的点的轨迹是双曲线;
(c > a >0)的点的轨迹是双曲线;
④到定点F(c,0)和定直线x=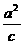 的距离之比为
的距离之比为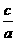 (a > c>0)的动点轨迹是椭圆;
(a > c>0)的动点轨迹是椭圆;
请将正确命题的代号都填在横线上 。
联想:(1)抛物线y2 = 4x的焦点为F,准线交x轴于R点,过抛物线上一点P(4,4)作PQ⊥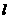 于Q,则梯形PQRF的面积是 ( )
于Q,则梯形PQRF的面积是 ( )
A.12 B.14 C.16 D.18
(2)过椭圆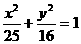 左焦点F的直线交椭圆于A、B两点
左焦点F的直线交椭圆于A、B两点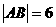 过A、B分别作左准线
过A、B分别作左准线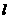 的垂线AA1⊥
的垂线AA1⊥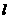 于A1,BB1⊥
于A1,BB1⊥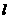 于B1,以
于B1,以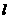 轴将椭圆在空中旋转1200,则线段AB所扫过的曲面面积为
。
轴将椭圆在空中旋转1200,则线段AB所扫过的曲面面积为
。
(3)已知点A(3,2),F(2,0),在双曲线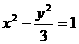 上求一点P,其坐标为 时,
上求一点P,其坐标为 时,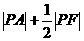 的值最小。
的值最小。
5.如果平面α外的两条异面直线a、b在平面α上的射影是两条平行直线,那么直线a、b与平面α的位置关系是( )
A.仅有一条直线与平面α相交 B.两条直线都与平面相交
C.两条直线都与平面α相交 D.至少有一条直线与平面α相交
联想:(1)P为异面直线a、b外任一点,过P与a、b都平行的平面有( )
A.唯一一个 B.恰好两个 C.至多一个 D.至少一个
(2)过平面外一直线作该平面的平行平面( )
A.只可能作一个 B.至少作一个 C.至多作一个 D.这样的平面不存在
(3)a、b是两异面直线,下列结论正确的是 ( )
A.过不在a、b上的任一点,可作一个平面与a、b都平行
B.过不在a、b上的任一点,可作一条直线与a、b都相交
C.过不在a、b上的任一点,可作一条直线与a、b都平行
D.过a可以并且只可以作一个平面与b平行
3.设sin (α+2β)=5sinα,则tan(α+β):tanβ= 。
联想:(1)已知:tan(α+β) =4,tan(α-β)=2,那么tan2α= .
(2)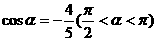 ,tan
,tan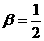 ,则
,则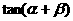 之值为
。
之值为
。
(3)已知: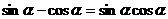 ,则
,则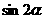 的值为( )
的值为( )
A.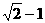 B.
B.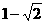 C.
C.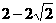 D.
D.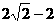
(4)在△ABC中,若sinA=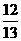 ,cosB=
,cosB=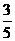 ,则cosC的值为( )
,则cosC的值为( )
A.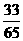 B.
B.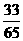 或
或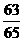 C.-
C.-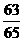 D.-
D.-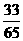 或-
或-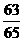 4.不等式(
4.不等式(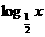 )2<
)2<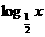 2的解集为
.
2的解集为
.
联想(1)不等式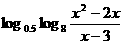 <0的解集为
.
<0的解集为
.
(2)不等式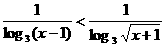 的解集为( )
的解集为( )
A.(3,+∞) B.(0,3) C.(1,2) D.(1,2)∪(3,+∞)
(3)已知定义在R上的偶函数f (x)在x∈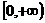 上是增函数,且f (
上是增函数,且f (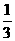 )=0,则满足f (
)=0,则满足f (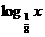 )>0的x的取值范围是( )
)>0的x的取值范围是( )
A.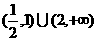 B.
B.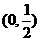 C.
C.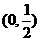
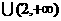 D.
D.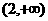
(4)不等式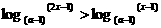 成立的充要条件是( )
成立的充要条件是( )
A.a>2,x>1 B.a>1,x>1 C.a>2,x>0 D.x>0
2.函数f (x)=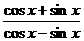 的最小正周期为( )
的最小正周期为( )
A.2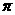 B.
B.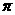 C.
C.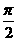 D.以上都不对
D.以上都不对
联想:(1)函数f (x)=sin(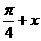 )·cos(
)·cos(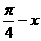 )的最小周期为( )
)的最小周期为( )
A.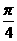 B.
B.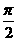 C.
C.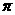 D.2
D.2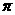
(2)函数y=sin6x+cos6x的最小正周期为 。
(3)函数y=tan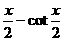 的最小正周期为 。
的最小正周期为 。
(4)已知函数f (x)是以2为周期的偶函数且当x∈(0,1)时,f (x)=x+1,则f (x)在(1,2)上的解析式是( )
A.f (x)=1-x B.f (x)=3-x C.f (x)=x-3 D.f (x)=-x-1
1.函数f (x)=log0.5(sinxcosx)的单调递减区间是(以下k∈Z)( )
A.(k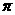 -
-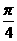 ,k
,k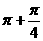 )
B.
)
B.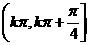
C.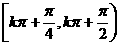 D.
D.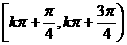
联想:(1)函数y=cos(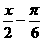 )
)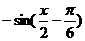 的单调递增区间为( )
的单调递增区间为( )
A.[4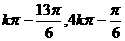 ]
B.[
]
B.[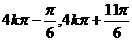 ]
]
C.[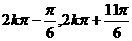 ]
D.[
]
D.[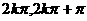 ] (以上k∈Z)
] (以上k∈Z)
(2)函数f (x)=lg(sinx-cosx)的单调递减区间为 。
14.设数列{an}的前n项和为Sn,且a2≠a1,证明:{an}是首项为1的等比数列的充要条件是存在非零常数a,b满足Sn=a+ban且a+b=1
联想:数列{an}中,其前n项和为Sn,当n≥1时,Sn+1是an+1与Sn+1+k的等比中项(k≠0)
(I)求证:对于n≥1有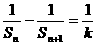
(II)设a1=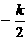 ,求Sn的表达式。
,求Sn的表达式。
(III)设a1=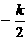 ,且{
,且{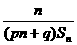 }成等差数列,求证:
}成等差数列,求证: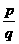 是与k无关的常数。
是与k无关的常数。
联想与激活(2)
13.袋内有9个白球和3个红球,从袋内任意地顺次取出三个球(取出后不放回)。
(I)求第三次取出的球是白球的概率
(II)当第三次取出的球是白球时,问第一次取出的球是白球的概率是多少?
联想:如图,已知电路中4个开关闭合的概率都是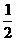 ,
,
且是相互独立的,求灯亮的概率。
12.某纯净水制造厂在净化水过程中,每增加一次过滤可减少水中杂质20%,要使水中杂质减少到原来的5%以下,则至少需过滤的次数为( )
A.5 B.10 C.14 D.15
联想:某公司一月份推出新产品A,成本为400元/件,经试销调查,销售量与销售价的关系如下表:
|
销售价(x元/件) |
650 |
662 |
719 |
800 |
900 |
|
销售量(y件) |
350 |
338 |
281 |
200 |
100 |
据此,写出x与y可满足的一个函数关系式 ;
 并据此,应将销售价定为
元时,利润最大。
并据此,应将销售价定为
元时,利润最大。
11.椭圆的一个焦点为圆心,焦距为半径的圆过椭圆的两个顶点,则此椭圆的离心率e= 。
联想:(1)双曲线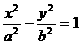 中,左焦点为F,右顶点为A,虚轴顶点为B,若BF⊥AB,则离心率e=
。
中,左焦点为F,右顶点为A,虚轴顶点为B,若BF⊥AB,则离心率e=
。
(2)椭圆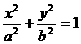 (a>b>0)的两个顶点A(a,0),B(0,b),若右焦点F到直线AB的距离为
(a>b>0)的两个顶点A(a,0),B(0,b),若右焦点F到直线AB的距离为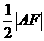 ,则离心率e= 。
,则离心率e= 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com