
题目列表(包括答案和解析)
1.设集合A={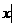
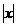 ≤4,x
≤4,x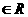 },B={
},B={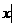
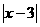 ≤a,x
≤a,x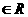 },若A
},若A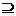 B,则实数a的取值范围为 ( )
B,则实数a的取值范围为 ( )
A.0≤a≤1 B.a≤1 C.a<1 D.0<a<1
联想:(1)A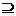 B是
B是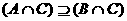 成立的
条件
成立的
条件
(2)已知集合A={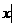 x2-a<0},B={
x2-a<0},B={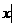 x < 2},若A
x < 2},若A B=A,则实数a的取值范围是
B=A,则实数a的取值范围是
(3)函数f ( x )是定义在R上的减函数,图象经过点A(0,4)和点B(3,-2),且不等式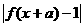 <3的解集为(-1,2),则实数a的值为( )
<3的解集为(-1,2),则实数a的值为( )
A.1 B.-1 C.2 D.-2
(4)有以下四个命题:CuA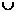 B=U(U为全集);A
B=U(U为全集);A B=A;A
B=A;A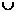 B=B;CuA
B=B;CuA B=
B=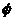 ,这中间与命题:A
,这中间与命题:A B等价的有 ( )
B等价的有 ( )
A.1个 B.2个 C.3个 D.4个
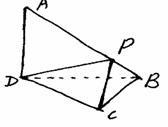
12.如图所示,△ADB和△CBD都是等腰直角三角形。
且它们所在的平面互相垂直,∠ADB=∠CBD=90°,AD=a.
(I)求异面直线AD,BC所成的角; (II)设P是线段
AB上的动点,问P、B两点间的距离多少时, △PCD与
△BCD所在平面成45°角?
(III)证明:A、B、C、D四点所在球面的面积为S,求S的值。
联想与激活(4)
11.这是一个计算机程序的操作说明:
① 初始值x=1,y=1,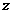 =0, n=0;
=0, n=0;
② n=n+1.(将当前n+1的值赋予新的n);
③ x=x+2(将当前x+2的值赋予新的x);
④ y=2y(将当前2y的值赋予新的y);
⑤ z=z +xy(将当前z+xy的值赋予新的z);
⑥ 如果z>7000,则执行语句⑦,否则回语句②继续进行;
⑦ 打印n,z;
⑧ 程序终止。由语句⑦打印出的数值为____________,___________.(要写出计算过程)
联想:已知数列{an}中,a1=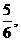 且对任意自然数n都有an+1=
且对任意自然数n都有an+1=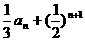 ,数列{bn}对任意自然数n都有bn = an+1-
,数列{bn}对任意自然数n都有bn = an+1-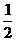 an
an
(I) 求证数列{bn}是等比数列; (II)求数列{an}的通项公式;
 (III)设数列{an}前n项的和为Sn,求
(III)设数列{an}前n项的和为Sn,求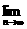 Sn的值。
Sn的值。
10.设双曲线的左、右焦点为F1、F2,左右两顶点为M、N,若△PF1F2的一个顶点P在双曲线上,则△PF1F2的内切圆与边F1F2的切点的位置是( )
A.在线段MN的内部 B.在线段F1M内部或F2N的内部
C.点N或M D.以上三种情况都有可能
联想:(1)设F1,F2是椭圆的两上焦点,P为椭圆上一点,且∠F1PF2=60°,则离心率e的范围是__________________。
(2)若F2是椭圆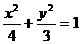 的右焦点,点A坐标为(1,1),则在椭圆上使2
的右焦点,点A坐标为(1,1),则在椭圆上使2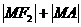 的值最小的点M的坐标是( )
的值最小的点M的坐标是( )
A.(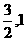 ) B.
) B.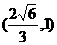 C.(2,0) D.(1,
C.(2,0) D.(1,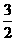 )
)
9.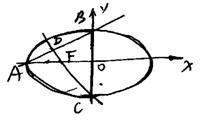 如图,椭圆
如图,椭圆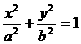 (a>b>o)的离心率e=
(a>b>o)的离心率e=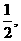 左焦点为F,A,B,C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )
左焦点为F,A,B,C为其三个顶点,直线CF与AB交于D,则tan∠BDC的值等于( )
A.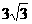 B.
B.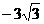
C.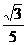 D.
D.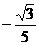
联想:(1)设双曲线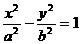 的一条准线与两条渐近线交于A、B两点,相应的焦点为F,若以AB为直径的圆恰好过F点,则离心率为(
)
的一条准线与两条渐近线交于A、B两点,相应的焦点为F,若以AB为直径的圆恰好过F点,则离心率为(
)
A.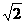 B.
B.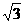 C.2
D.
C.2
D.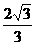
(2)双曲线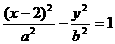 (a>0,b>0)的一条准线被它的两条渐近线截得线段的长度等于它的一个焦点到一条渐近线的距离,则双曲线的两条渐近线的夹角为(
)
(a>0,b>0)的一条准线被它的两条渐近线截得线段的长度等于它的一个焦点到一条渐近线的距离,则双曲线的两条渐近线的夹角为(
)
A.30° B.60° C.45° D.90°
8.已知a+b>0,b=4a,(a+b)n展开式按a的降幂排列,其中第n项与第n-1项相等,那么正整数n等于( )
A.4 B.9 C.10 D.11
联想:(1)在(x2+x-2)5的展开式中,x的系数是________________.
(2)已知(x+1)6(ax-1)2展开式中含x3项的系数为20,则实数a的值为______________.
(3) 若(1+2x)100=a0+a1(x-1)+a2(x-1)2+…+a100(x-1)100,则a1+a3+a5+…+a99=______________.
7.设函数f(x)=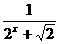 ,利用课本中推导等差数列前n项和的公式的方法,可求得
,利用课本中推导等差数列前n项和的公式的方法,可求得
f(-5)+f(-4)+…+f(0)+…+f(5)+f(6)的值为_______________________.
联想:(1)已知函数f(x)=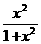 ,那么
,那么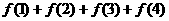 +
+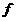 (
(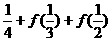 的值为___________________________。
的值为___________________________。
(2)已知函数f(x)满足:f(p+ q)=f(p)·f( q ),f(1)=3,则
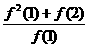 +
+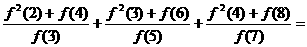 _____________________
_____________________
(3)对于定义在实数集R上的函数f(x),如果存在实数x0, 使f(x0)=x0,那么x0叫做函数f(x)的一个不动点。已知,函数f(x)=x2+2ax+1不存在不动点,那么实数a的取值范围是( )
A.(-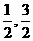 )
B.(
)
B.(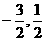 )
C.(-1,1) D.(-
)
C.(-1,1) D.(-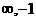 )v(1+
)v(1+ )
)
6.在等差数列{an}中,a10<0 ,a11
>0 ,且a11>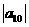 ,数列{an}的前n项和为Sn,则使Sn<0的n的最大值是( )
,数列{an}的前n项和为Sn,则使Sn<0的n的最大值是( )
A.19 B.20 C.21 D.无穷大
联想:(1)在A·P{an}中,若a4+a6+a8+a10+a12=120, 则2a10-a12的值为( )
A.20 B.22 C.24 D.28
(2)若正数a、b、c依次构成公比大于1的等比数列,当x>1时,logax, logbx,logcx依次成( )
A.等差数列 B.等比数列 C.各项倒数成A·P D.各项倒数成G·P
(3)已知A·P{an},{bn}前n项和分别是Sn、Tn,若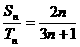 ,则
,则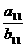 等于( )
等于( )
A.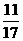 B.
B.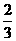 C.
C.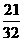 D.
D.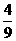
5.若以连续掷两次骰子分别得到的点数m、n分为点P的坐标,则点P落在圆x2+y2=16内的概率为( )
A.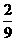 B.
B. C.
C.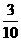 D.
D.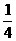
联想:(1)有红、黄、蓝三种颜色的旗帜各3面,在每种颜色的3面旗帜上分别标上号码1、2和3。现在取出3面,它们的颜色与号码均不相同的概率是 。
(2)从集合{0,1,2,3,5,7,11}中任取3个元素分别作为方程Ax+By+C=0中的A、B、C所得恰好总经过坐标原点的直线的概率是 。
(3)袋内装有大小相同的4个白球和3个黑球,从中任意摸出3个球,其中只有一个黑球的概率是
。
(4)在大小相同的6个球中,2个是红球,4个是白球,若从中任意选取3个,则所选取的3个球中至少有一个红球的概率是 。
4.已知a、b是直线,α、β、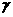 是平面。给出下列命题:①a∥α,a∥β,α∩β=b,则a∥b;②α⊥
是平面。给出下列命题:①a∥α,a∥β,α∩β=b,则a∥b;②α⊥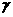 ,β⊥
,β⊥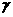 ,α∥β;③a⊥α,b⊥β,a⊥b,则α⊥β;④α∥β,β∥
,α∥β;③a⊥α,b⊥β,a⊥b,则α⊥β;④α∥β,β∥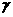 ,a⊥α,则a⊥
,a⊥α,则a⊥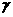 。其中正确命题的序号是( )
。其中正确命题的序号是( )
A.①②④ B.①③④ C.②④ D.②③
联想:(1)已知直线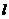 ⊥平面α,直线m
⊥平面α,直线m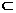 β,有下面四个命题:
β,有下面四个命题:
①α∥β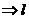 ⊥m;②α⊥β
⊥m;②α⊥β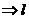 ∥m;③
∥m;③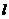 ∥m
∥m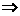 α⊥β;④
α⊥β;④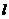 ∥m
∥m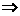 α∥β。其中正确的两个命题是( )
α∥β。其中正确的两个命题是( )
A.①与② B.③与④ C.②与④ D.①与③
(2)已知集合A、B、C,A={直线},B={平面},C=A∪B若a∈A,b∈B,c∈C,在下面命题中
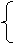
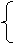
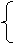
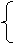 a⊥b
a⊥b
a∥b
a∥b
a⊥b
a⊥b
a∥b
a∥b
①  a∥c ②
a∥c ②
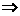 a⊥c ③
a⊥c ③ 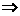 a∥c ④
a∥c ④ 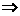 a⊥c
a⊥c
c⊥b c∥b b∥c c⊥b
正确命题的序号是 。(注:把你认为正确的序号都填上)
(3)若a、b是两条异面直线,则存在惟一的平面β,满足( )
A.a∥β且b∥β B.a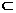 β且b∥β C.a⊥β且b⊥β D.a
β且b∥β C.a⊥β且b⊥β D.a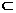 β且b⊥β
β且b⊥β
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com