
题目列表(包括答案和解析)
3. 直线与平面平行的性质定理:
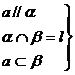
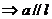
[典型例题]
[例1] 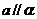 ,
,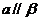 ,
, ,求证:
,求证: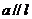 。
。
证:过 作
作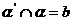
∴ 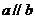
过 作
作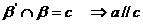
∴ 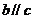
∴
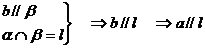
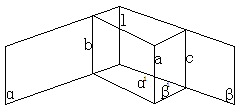
[例2]  、
、 异面,求证过
异面,求证过 与
与 平行的平面有且仅有一个。
平行的平面有且仅有一个。
证:存在性,过 上一点
上一点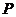 作直线
作直线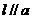
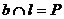 确立平面
确立平面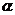
∴ 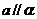
唯一性,假设存在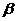 ,
,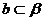 ,
,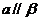
∴
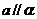 ,
,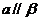 ,
,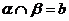
由例1
∴
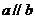 与已知矛盾
与已知矛盾
∴ 只有一个
[例3] 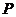 为空间一点,
为空间一点, 、
、 异面,过
异面,过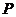 作与
作与 、
、 均平行的平面可作
均平行的平面可作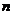 个。
个。
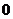 个或
个或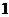 个,过
个,过 存在平面
存在平面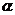 ,
,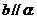 。
。
过 存在平面
存在平面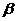 ,
,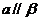 。
。
① 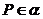 或
或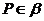
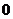 个
个
② 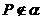 且
且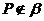
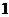 个
个
可用反证法证明只有一个。
[例4] 正方形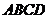 交正方形
交正方形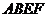 于
于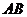 ,
,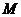 、
、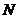 在对角线
在对角线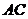 、
、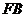 上,且
上,且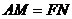 ,求证:
,求证: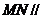 平面
平面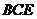 。
。
证:过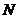 作
作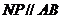 交
交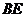 于
于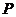
过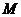 作
作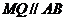 交
交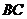 于
于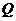
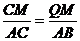 ,
,
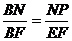
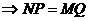
 又∵
又∵ 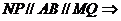
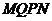
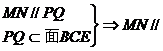 面
面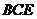
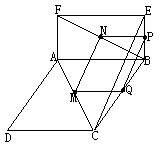
[例5] 如图,异面直线 、
、 ,
,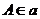 ,
,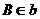 ,
,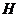 为
为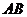 中点,
中点,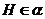 ,
,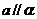 ,
,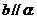 ,
,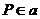 ,
,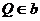 ,
,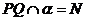 ,求:
,求: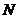 为
为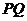 中点。
中点。
证:连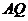 交
交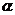 于
于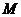 ,连
,连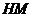 、
、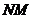
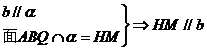
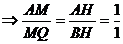
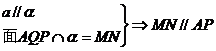
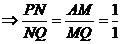
∴ 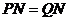
[例6] 三个平面两两相交不共线,求证三条直线交于一点或两两平行。
证:设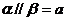 ,
,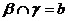 ,
,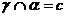
∴  、
、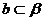
(1)若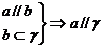
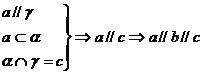
(2)若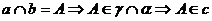
∴
 、
、 、
、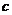 交于一点
交于一点
 [例7]
[例7] 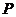 为
为 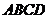 所在平面外一点,
所在平面外一点,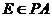 ,
,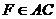 ,且
,且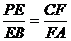 ,求证:
,求证: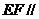 面
面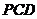 。
。
证:连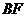 交
交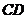 于
于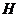 ,连
,连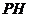 ,
,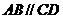
∴
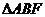 ∽
∽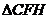
∴
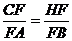
在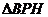 中,
中,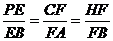
∴
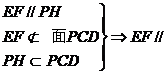 面
面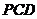
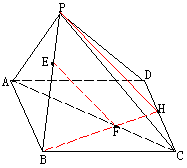
[例8]  、
、 异面直线,
异面直线,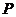 为空间任一点,过
为空间任一点,过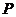 作直线
作直线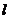 与
与 、
、 均相交,这样的直线可以作多少条。
均相交,这样的直线可以作多少条。
解: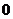 ,
,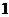 或无数。
或无数。
过 存在唯一个平面
存在唯一个平面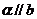
过 存在唯一个平面
存在唯一个平面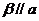
① 若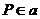 或
或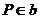 ,有无数条
,有无数条
②
若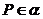 或
或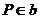 ,且
,且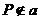 且
且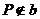
直线不存在
③
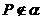 且
且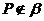 ,有且只有一条。
,有且只有一条。
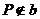 ,过
,过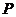 、
、 作平面
作平面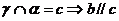
∴
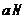
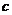
∴
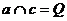
连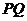 与
与 相交
相交
∴
存在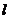 与
与 、
、 均相交
均相交
假设有两条过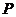 的直线
的直线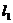 、
、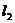 与
与 、
、 均相交
均相交
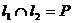 ,确立平面
,确立平面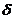
 与
与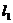 、
、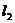 各有一个交点
各有一个交点
∴
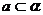
同理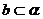 ,与
,与 、
、 异面矛盾
异面矛盾
∴ 假设不成立
∴ 只有一条
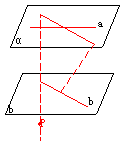
[例9]  、
、 、
、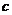 两两异面,空间与
两两异面,空间与 、
、 、
、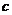 ,均相交的直线有多少条?
,均相交的直线有多少条?
证:存在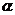 ,
,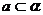 ,
,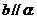 ,
,
存在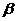 ,
,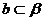 ,
,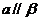
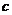 与
与 、
、 异面,
异面,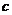 中有无数个点在
中有无数个点在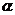 、
、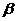 外
外
每一个点可作一条线与 、
、 均相交
均相交
∴ 无数条
[模拟试题]
2. 直线与平面平行的判定定理:
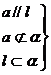
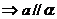
1. 直线平面的位置关系:
(1)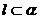 ,直线在平面内,有无数个公共点,
,直线在平面内,有无数个公共点,
(2)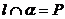 ,直线与平面相交,只有一个公共点。
,直线与平面相交,只有一个公共点。
(3)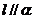 ,直线与平面平行,无公共点。
,直线与平面平行,无公共点。
直线与平面平行
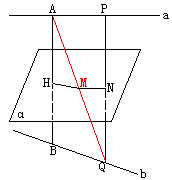
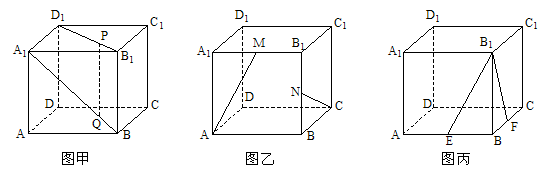
20. 在棱长为1的正方体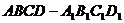 中
中
(1)P、Q分别是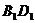 、
、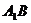 上的点且
上的点且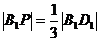 ,
,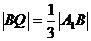 (如图甲)。求证:PQ//平面
(如图甲)。求证:PQ//平面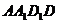
(2)M、N分别是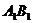 、
、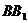 的中点(如图乙),求直线AM与CN所成的角
的中点(如图乙),求直线AM与CN所成的角
(3)E、F分别是AB、BC的中点(如图丙),试问在棱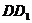 上能否找到一点H,使
上能否找到一点H,使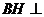 平面
平面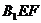 ?若能,试确定点H的位置,若不能,请说明理由。
?若能,试确定点H的位置,若不能,请说明理由。
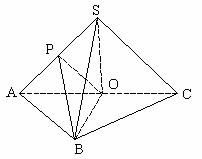
19. 已知S是 所在平面外一点,O是边AC的中点,
所在平面外一点,O是边AC的中点,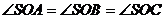 ,点P是SA的中点。
,点P是SA的中点。
(1)求证: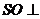 平面ABC
平面ABC
(2)求证: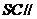 平面BOP
平面BOP
(3)若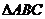 是等腰直角三角形,且
是等腰直角三角形,且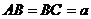 ,又SC与平面BOP的距离为
,又SC与平面BOP的距离为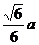 ,求二面角
,求二面角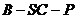 的大小。
的大小。
18. 如图,直三棱柱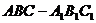 中,
中,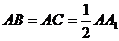 ,
,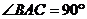 ,D为棱
,D为棱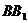 的中点。
的中点。
(1)求异面直线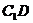 与
与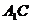 所成的角;
所成的角;
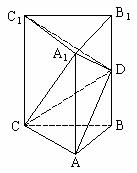
(2)求证:平面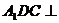 平面ADC
平面ADC
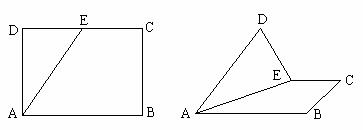
17. 在矩形ABCD中,AB=4,BC=3,E为DC边的中点,沿AE将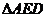 折起,使二面角
折起,使二面角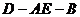 为
为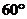 。
。
(1)求DE与平面AC 所成角的大小
(2)求二面角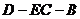 的大小
的大小
16. 已知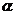 、
、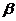 是两个不同的平面,
是两个不同的平面,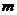 ,
,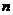 是平面
是平面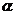 及
及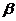 之外的两条不同直线,给出四个论断:①
之外的两条不同直线,给出四个论断:① 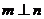 ;②
;② 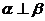 ;③
;③ 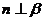 ;④
;④ 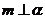 。以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题:
。
。以其中三个论断作为条件,余下的一个论断作为结论,写出你认为正确的一个命题:
。
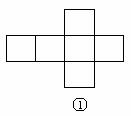
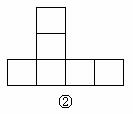
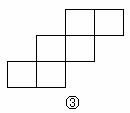
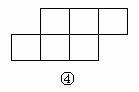
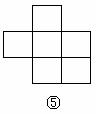
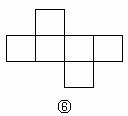
15. 如下图,在下列六个图形中,每个小四边形皆为全等的正方形,那么沿其正方形相邻边折叠,能够围成正方体的是 (要求:把你认为正确图形的序号都填上)。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com