
题目列表(包括答案和解析)
(1)空间几何体
① 认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.
② 能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述的三视图所表示的立体模型,会用斜二测法画出它们的直观图.
③ 会用平行投影与中心投影两种方法,画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.
④ 会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不作严格要求).
⑤ 了解球、棱柱、棱锥、台的表面积和体积的计算公式(不要求记忆公式).
注重培养学生的空间想象能力,画出简单空间图形的三视图与直观图,且会把三视图、直观图还原成空间图形。例如07年广东高考文科第17题:

(2)点、直线、平面之间的位置关系
① 理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理.
◆公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点在此平面内.
◆公理2:过不在同一条直线上的三点,有且只有一个平面.
◆公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.
◆公理4:平行于同一条直线的两条直线互相平行.
◆定理:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.
② 以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定.
理解以下判定定理.
◆如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.
◆如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.
◆如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.
◆如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.
理解以下性质定理,并能够证明.
◆如果一条直线与一个平面平行,经过该直线的任一个平面与此平面相交,那么这条直线就和交线平行.
◆如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行.
◆垂直于同一个平面的两条直线平行.
◆如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直.
③ 能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.
注重线面关系(线线平行、线面平行、面面平行之间的转移;线线垂直、线面垂直、面面垂直之间的转移;还有平行与垂直关系的转移)。例如07年广东高考文科第6题:

再如06年北京高考题:如图,在底面为平行四边形的四棱锥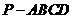 中,
中,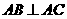 ,
,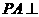 平面
平面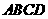 ,且
,且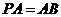 ,点
,点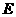 是
是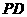 的中点.
的中点.
(Ⅰ)求证: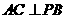 ;
;
(Ⅱ)求证: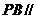 平面
平面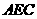 ;
;
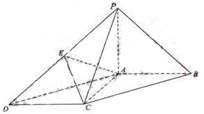 (Ⅲ)求二面角
(Ⅲ)求二面角 的大小.
的大小.
解:(1)由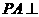 平面
平面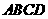 可得PA^AC
可得PA^AC
又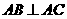 ,所以AC^平面PAB,所以
,所以AC^平面PAB,所以
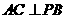
(2)如图,连BD交AC于点O,连EO,则
EO是△PDB的中位线,\EO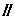 PB
PB
\PB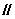 平面
平面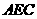
19、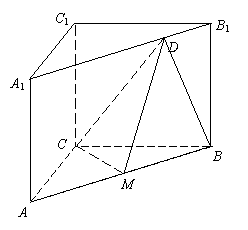 如图,在直三棱柱
如图,在直三棱柱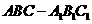 中,
中,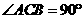 ,
,
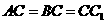 ,
,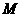 为
为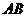 的中点,D在A1B1上
的中点,D在A1B1上
且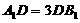 .
.
(I)求证:平面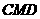 ⊥平面
⊥平面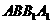 ;
;
(II)求二面角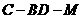 的大小.
的大小.
18、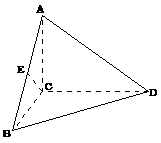 如图:已知在
如图:已知在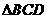 中,
中,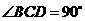 ,
,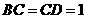 ,
,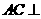 平面
平面 ,
,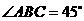 ,
,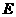 是
是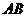 的中点.
的中点.
(1)求直线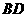 和
和 所成的角;
所成的角;
(2)求点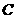 到平面
到平面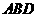 的距离;
的距离;
(3)若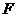 是线段
是线段 上的一个动点,请确定点
上的一个动点,请确定点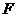 的
的
位置,使得平面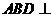 平面
平面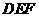 .
.
16、矩形ABCD中,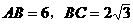 ,沿对角线BD将三角形ABD向上折起,使点A移动到点P,使点P在平面BCD上的射影在DC上(如下图F)。
,沿对角线BD将三角形ABD向上折起,使点A移动到点P,使点P在平面BCD上的射影在DC上(如下图F)。
(I)求证:PD⊥PC;
(II)求二面角P-DB-C的大小;
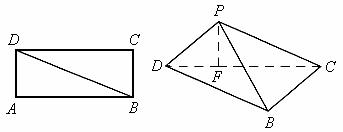 (III)求直线CD与平面PBD所成角的大小。
(III)求直线CD与平面PBD所成角的大小。
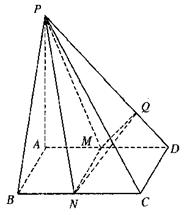 17、已知四棱锥P-ABCD(如图),底面是边长为2的正方形. 侧棱PA⊥底面ABCD,M、N分别为AD、BC的中点. MQ⊥PD于Q,直线PC与平面PBA所成角的正弦值为
17、已知四棱锥P-ABCD(如图),底面是边长为2的正方形. 侧棱PA⊥底面ABCD,M、N分别为AD、BC的中点. MQ⊥PD于Q,直线PC与平面PBA所成角的正弦值为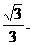
(Ⅰ)求证:平面PMN⊥平面PAD;
(Ⅱ)求PA的长;
(Ⅲ)求二面角P-MN-Q的余弦值.
15、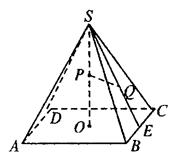 如图,已知正四棱锥
如图,已知正四棱锥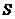 -
-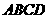 的底面边长为4,高为6,点
的底面边长为4,高为6,点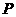 是高的中点,点
是高的中点,点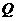 是侧面
是侧面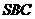 的重心.求:
的重心.求:
(1)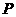 、
、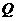 两点间的距离;
两点间的距离;
(2)异面直线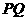 与
与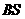 所成角的余弦值;
所成角的余弦值;
(3)直线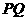 与底面
与底面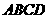 所成的角.
所成的角.
14、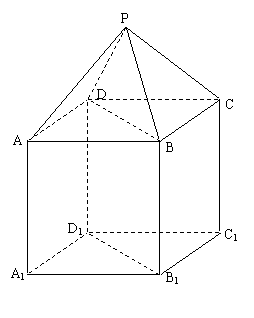 如图,P-ABCD是正四棱锥,
如图,P-ABCD是正四棱锥,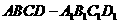
是正方体,其中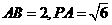 。
。
(1)求证: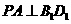 ;
;
(2)求平面PAD与平面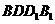 所成的锐二面角
所成的锐二面角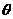 的
的
大小。
13、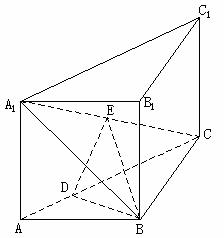 如图:直三棱柱ABC-A1B1C1中,
如图:直三棱柱ABC-A1B1C1中,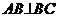 ,E是A1C的中点,
,E是A1C的中点,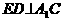 且交AC于D,
且交AC于D,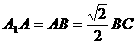 。
。
(I)证明: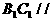 平面
平面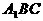 ;
;
(II)证明: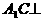 平面
平面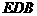 ;
;
(III)求平面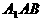 与平面EDB所成的二面角
与平面EDB所成的二面角
的大小(仅考虑平面角为锐角的情况)。
12、如图,矩形ABCD中,DC=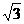 ,AD=1,在DC上截取DE=1,
,AD=1,在DC上截取DE=1,
将△ADE沿AE翻折到D1点,点D1在平面ABC上的射影落在
AC上时,二面角D1-AE-B的平面角的余弦值是 .
10、锥体体积V可以由底面积S与高h求得: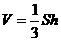 . 已知正三棱锥P-ABC底面边长为2
. 已知正三棱锥P-ABC底面边长为2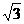 ,体积为4
,体积为4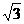 ,则底面三角形ABC的中心O到侧面PAB的距离为 .
,则底面三角形ABC的中心O到侧面PAB的距离为 .
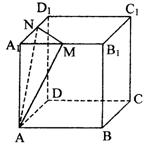 11、如图,在棱长为3的正方体ABCD-A1B1C1D1中,
11、如图,在棱长为3的正方体ABCD-A1B1C1D1中,
M、N分别是棱A1B1、A1D1的中点,则点B到平
面AMN的距离是 ( )
A.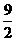 B.
B.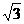
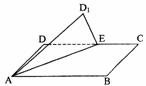 C.
C.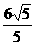 D.2
D.2
9、P是正三棱柱ABC-A1B1C1的侧棱CC1上一点(侧棱端点除外),则∠APB的大小满足:
A.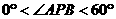 B.
B.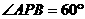
C.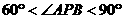 D.以上都有可能
D.以上都有可能
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com