
题目列表(包括答案和解析)
7. 将直线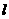 沿
沿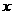 轴正向平移2个单位,再沿
轴正向平移2个单位,再沿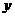 轴负方向平移3个单位,又回到了原来的位置,则
轴负方向平移3个单位,又回到了原来的位置,则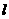 的斜率为( )
的斜率为( )
A. 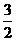 B.
B. 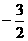 C.
C. 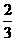 D.
D. 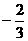
6. 直线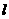 过点
过点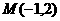 ,且与以
,且与以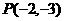 和
和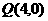 为端点的线段相交,则
为端点的线段相交,则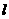 斜率取值范围为( )
斜率取值范围为( )
A. 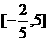 B.
B. 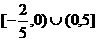 C.
C. 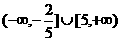 D. 以上都不对
D. 以上都不对
5. 三条直线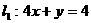 ;
;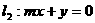 ;
;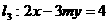 不能围成三角形,则
不能围成三角形,则 取值的个数为( )
取值的个数为( )
A.  B.
B. 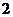 C.
C. 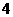 D.
D. 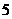
4. 已知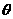 为直线
为直线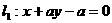 和
和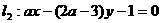 所成的角,则当
所成的角,则当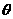 取最大值时,实数
取最大值时,实数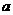 值为( )
值为( )
A. 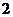 B.
B. 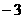 或
或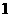 C.
C. 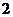 或
或 D.
D. 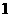 或
或
3. 过原点,且与直线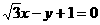 成
成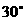 角的直线方程为( )
角的直线方程为( )
A. 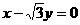 B.
B. 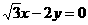 C.
C. 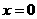 或
或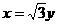 D.
D. 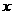
2. 若直线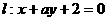 与直线
与直线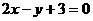 平行,则
平行,则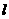 在两坐标轴上截距之和为( )
在两坐标轴上截距之和为( )
A. 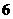 B.
B. 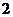 C.
C. 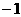 D.
D. 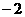
1. 直线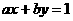 与两坐标轴围成的三角形面积为( )
与两坐标轴围成的三角形面积为( )
A. 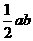 B.
B. 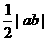 C.
C. 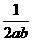 D.
D. 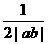
(五)线性规划
1. 二元一次不等式表示平面区域
(1)二元一次不等式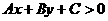 在平面直角坐标系中表示直线
在平面直角坐标系中表示直线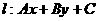
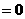 一侧所有点组成的平面区域,直线
一侧所有点组成的平面区域,直线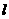 应画成虚线,
应画成虚线,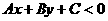 表示直线
表示直线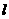 另一侧所有点组成的平面区域,画不等式。
另一侧所有点组成的平面区域,画不等式。 所表示的平面区域时,应把边界直线画成实线。
所表示的平面区域时,应把边界直线画成实线。
(2)二元一次不等式组所表示的平面区域是各个不等式表示的平面点集的交集即各个不等式所表示的平面区域的公共部分。
快捷判断法:
(1)代点检验法
(2)直线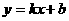 上半平面为
上半平面为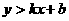 的区域;下半平面为
的区域;下半平面为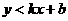 的区域
的区域
2. 线性规划
(1)对于变量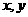 的约束条件,都是关于
的约束条件,都是关于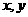 的一次不等式,称为线性约束条件,
的一次不等式,称为线性约束条件,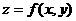 是欲达到最值所涉及的变量
是欲达到最值所涉及的变量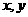 的解析式,叫做目标函数。当
的解析式,叫做目标函数。当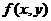 是关于
是关于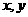 的一次解析式时,
的一次解析式时,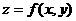 叫做线性目标函数。
叫做线性目标函数。
(2)求线性目标函数在线性约束条件下的最值问题称为线性规划问题,满足线性约束条件的解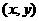 称为可行解。由所有解组成的集合叫可行域,使目标函数取得最值的可行解叫最优解。
称为可行解。由所有解组成的集合叫可行域,使目标函数取得最值的可行解叫最优解。
3. 求解线性规划问题的步骤是:(1)根据实际问题的约束条件列出不等式;(2)作出可行域,写出目标函数;(3)确定目标函数的最优位置,从而获得最优解。
[模拟试题](答题时间:45分钟)
(四)对称性问题(专题)方法--相关点法
1. 对称分两大类
(1)关于点中心对称:点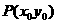 关于定点
关于定点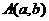 中心对称点
中心对称点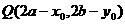
(2)关于直线轴对称:点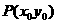 关于直线
关于直线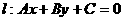 的对称点
的对称点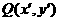 ,则
,则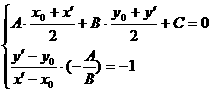 解出
解出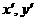 的值为:
的值为: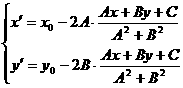
2. 常用对称的规律:已知点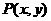 ,直线
,直线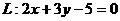
(1)关于X轴对称的对称点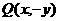 ;
;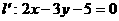
(2)关于Y轴对称的对称点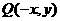 ;
;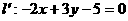
(3)关于直线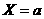 的对称点
的对称点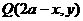 ;
;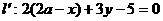
(4)关于直线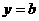 的对称点
的对称点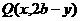 ;
;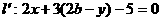
(5)关于原点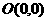 的对称点
的对称点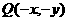 ;
;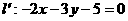
(6)关于点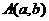 的对称点
的对称点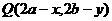 ;
;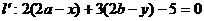
(7)关于直线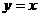 的对称点
的对称点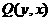 ;
;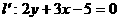
(8)关于直线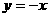 的对称点
的对称点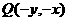 ;
;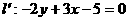
(9)关于直线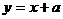 的对称点
的对称点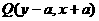 ;
;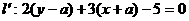
(10)关于直线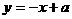 的对称点
的对称点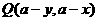 ;
;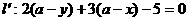
思考:我们注意到只须将对称点的坐标Q代入直线L即得对称的直线方程,为什么?
它们的理论依据是什么?--“相关点法”
我们以(9)题为例,即求直线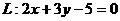 ,关于直线
,关于直线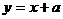 对称的直线方程。
对称的直线方程。
解:设所求直线上任意一点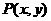
关于直线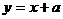 的对称点
的对称点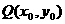
则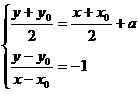 ∴
∴ 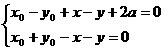 ∴
∴ 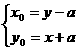
∵ 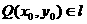 ∴
∴ 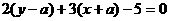 即:
即: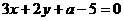
点拨:① 代入对称点坐标的理论依据是“相关点法”
② 有关对称性问题都可用“相关点法”求对称曲线。
(三)两条直线的位置关系
1. 判定两条直线的位置关系(三种:相交、平行、重合)
设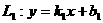 ;
;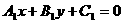
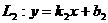 ;
;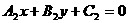
(1)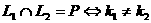 或仅有一个不存在
或仅有一个不存在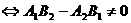
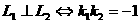 或一个为零一个不存在
或一个为零一个不存在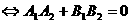
(2) 且
且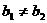 或
或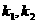 均不存在
均不存在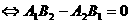 且
且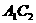
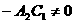
(3)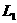 与
与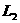 重合
重合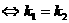 且
且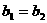 或
或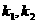 均不存在
均不存在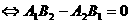 且
且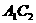
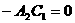
[例题] 已知两直线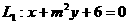 ;
;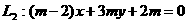 ,当
,当 为何值时,
为何值时,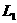 与
与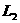 (1)相交(2)平行(3)重合
(1)相交(2)平行(3)重合
解:当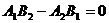 时,则
时,则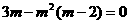 ∴
∴ 
(1)当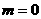 时,
时,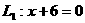 ;
;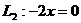 ∴
∴ 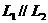
(2)当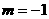 时,
时,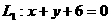 ;
;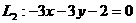 ∴
∴ 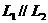
(3)当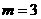 时,
时,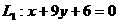 ;
;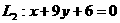 ∴
∴ 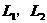 重合
重合
(4)当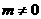 ,
,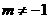 ,
,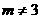 时,相交。
时,相交。
说明: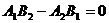 时,
时,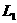 与
与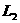 平行或重合相交且只有有数几个值应先分析。
平行或重合相交且只有有数几个值应先分析。
2. 两条直线所成的角(夹角)与直线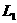 到
到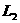 的角
的角
夹角: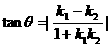
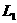 到
到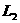 的角:
的角: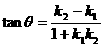
3. 点到直线的距离: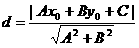
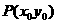 到
到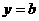 的距离为
的距离为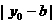 ;
;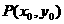 到
到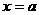 的距离为
的距离为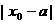 ,两条平行线
,两条平行线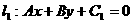 ;
;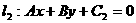 ,则
,则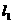 与
与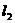 的距离
的距离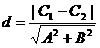
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com