
题目列表(包括答案和解析)
9. 如果直线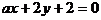 与直线
与直线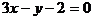 平行,那么系数a等于__________。
平行,那么系数a等于__________。
8. 已知过点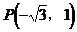 及Q(0,b)的直线的倾斜角介于120°与150°之间,则b的取值范围是______________。
及Q(0,b)的直线的倾斜角介于120°与150°之间,则b的取值范围是______________。
7. 从M(2,2)射出一条光线,经过x轴反射后过点N(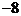 ,3),则反射点P的坐标为__________。
,3),则反射点P的坐标为__________。
6. 在约束条件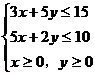 下,目标函数
下,目标函数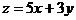 ( )
( )
A. 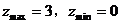 B.
B.
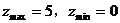
C. 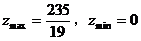 D.
D.
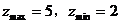
5. 点A(4,5)关于直线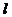 的对称点为
的对称点为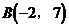 ,则
,则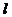 的方程为( )
的方程为( )
A.
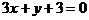 B.
B.
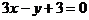
C.
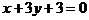 D.
D.
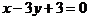
4. 已知两条直线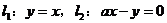 ,其中a为实数,当这两条直线的夹角在
,其中a为实数,当这两条直线的夹角在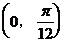 内变动时,a的取值范围是( )
内变动时,a的取值范围是( )
A.
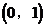 B.
B.
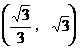
C.
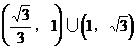 D.
D. 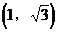
3. 直线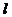 过点P(1,2)且与两坐标轴围成等腰三角形,则
过点P(1,2)且与两坐标轴围成等腰三角形,则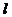 的方程为( )
的方程为( )
A. 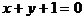 B.
B.
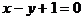 或
或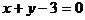
C. 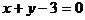 D.
D.
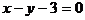 或
或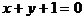
2. 经过点(10,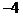 )且倾斜角的余弦值为
)且倾斜角的余弦值为 的直线方程是( )
的直线方程是( )
A.
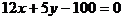 B.
B.
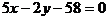
C.
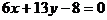 D.
D.
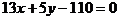
1. 直线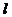 经过二、三、四象限,
经过二、三、四象限,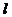 的倾斜角为
的倾斜角为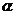 ,斜率为k,则( )
,斜率为k,则( )
A.  B.
B.
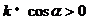
C.  D.
D.
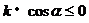
(三)简单的线性规划
1. 二元一次不等式表示平面区域
一般地,二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。
只需在此直线的某一侧取一特殊点(x0,y0)从Ax0+By0+C的正、负即可判断Ax+By+C>0表示直线哪一侧的区域。(若C≠0时,可取原点(0,0))

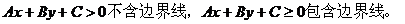
由几个不等式组成的不等式组所表示的平面区域,是各个不等式所表示的平面区域的公共部分。
2. 线性规划:
I. 基本概念:
(1)线性约束条件:
由x,y的一次不等式(或方程)组成的不等式组,是对x,y的约束条件。
(2)目标函数:
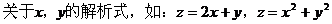
线性目标函数:关于x,y的一次解析式。
(3)可行解:满足线性约束条件的解(x,y)。
(4)可行域:所有可行解组成的集合。
(5)最优解:使目标函数达到最值的可行解。
(6)线性规划问题:求线性目标函数在约束条件下的最大(小)值问题。
II. 用图解法解线性规划的步骤:
(1)分析并将已知数据列出表格;
(2)确定约束条件;
(3)确定线性目标函数;
(4)画出可行域;
(5)利用线性目标函数,求出最优解;
(6)实际问题需要整数解时,应适当调整确定最优解。
例如:已知动点(x,y)所在区域是如图所示的阴影部分(包括边界),则目标函数z=x+2y的最小值和最大值分别为_____________。

解:作直线x+2y=0
平移此直线经过第一个点是(1,0)
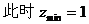
再往上平移到最后一点为(4,4)
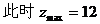
[典型例题]
例1. 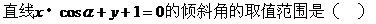


解析: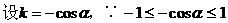
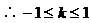
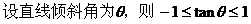
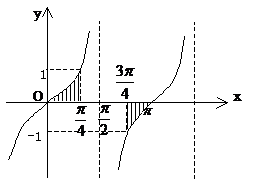
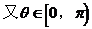
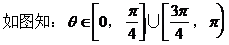
∴选C
例2. 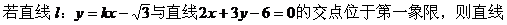
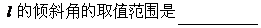
解析1:求出交点坐标,再由交点在第一象限求得斜率的范围,进而得到倾斜角的范围。
解析2: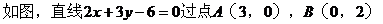
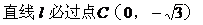


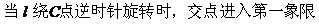
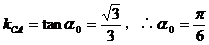
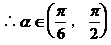
例3. 一条直线经过点P(2,3),并且分别满足下列条件,求直线方程:
(1)倾斜角是直线x-4y+3=0的倾斜角的2倍。
(2)与x,y轴的正半轴交于A、B两点,且△AOB的面积最小。
解:(1)设所求直线的倾斜角为θ,已知直线的倾斜角为α,则
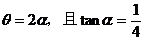
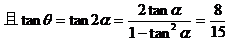

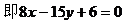
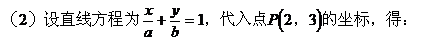
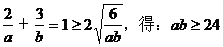
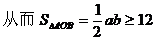
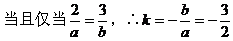
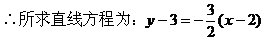
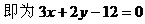
例4. 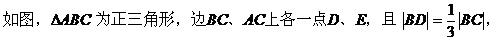
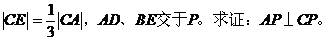

证明一:以B为坐标原点,直线BC为x轴,建立如图所示的直角坐标系。
取|BC|为单位长1,则各点坐标为:
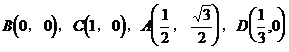
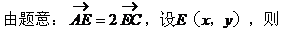
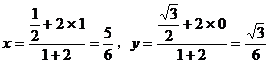
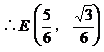
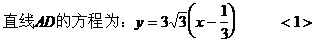
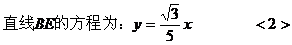

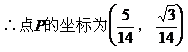
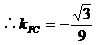
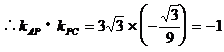
∴AP⊥CP
证明二:以B为坐标原点,直线BC为x轴,建立如图所示的直角坐标系,过D作DF∥BE交AC于F点,取|BC|为单位长1,则
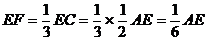

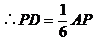
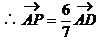
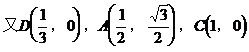
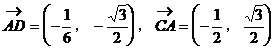
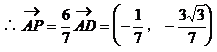
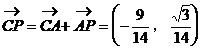
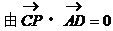
∴AP⊥CP
说明:数形结合强调的是将代数问题几何化,而解析法则是通过坐标系将几何问题代数化。
例5. 已知直线l1:mx+8y+n=0与l2:2x+my-1=0互相平行,求过点
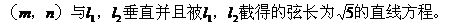
解: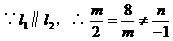
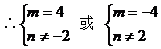
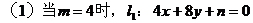
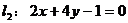
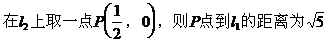
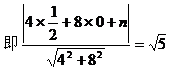
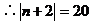
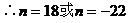
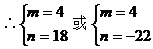

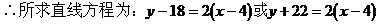
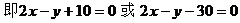
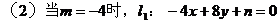
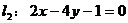
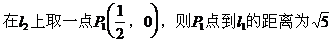
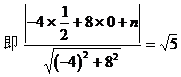
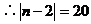
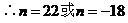
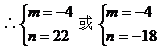
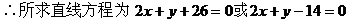
例6. 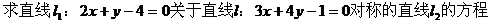
解: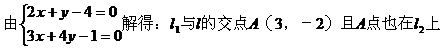
解法1:在直线l1上取一点B(2,0),设点B关于直线l的对称点C的坐标为C(x0,y0)
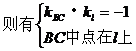
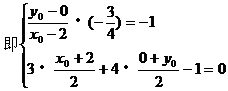
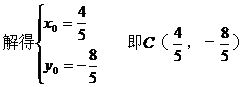
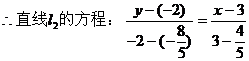
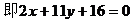

解法2: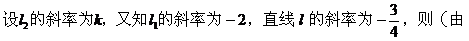
到角公式):
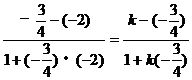
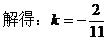
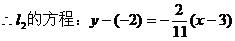
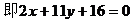
例7. 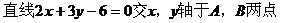
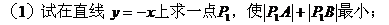
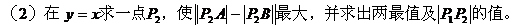
解: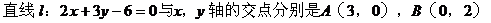
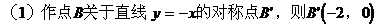
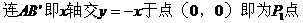
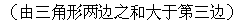
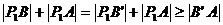
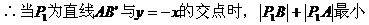
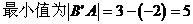

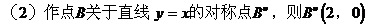
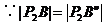
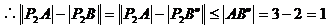
(由三角形两边之差小于第三边)
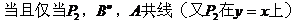
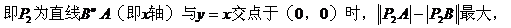
且为1。

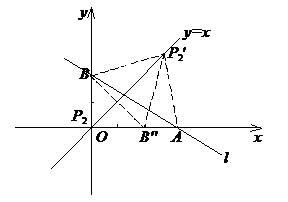
注:

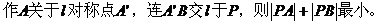
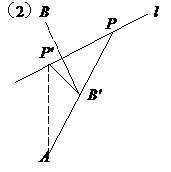
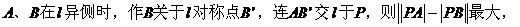
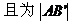
例8. 
A. 只能是(-3,0)
B. 只能是(0,6)
C. 只能是(-3,0)或(0,6)
D. 有无数个
解析: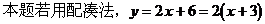
则平移向量为(-3,0),就可能误选A。
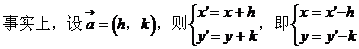
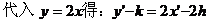
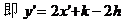
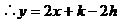
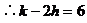
显然(h,k)不唯一确定
∴选D
例9. 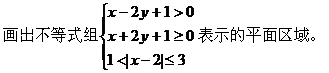
解: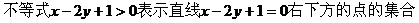
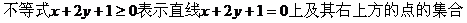
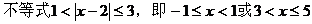
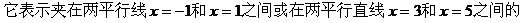
带状区域,但不包括直线x=1和x=3上的点。
所以,原不等式组表示的区域如图所示:

例10. 某工厂有甲、乙两种产品,计划每天各生产量不少于15t,已知生产甲产品1t,需煤9t,电力4kW·h,劳动力3个;生产乙产品1t需煤4t,电力5kW·h,劳动力10个。甲产品每1t利润7万元,乙产品每1t利润12万元,但每天用煤不超过300t,电力不超过200kW·h,劳动力只有300个,问每天各生产甲、乙两种产品多少,能使利润总额达到最大?
分析:将已知数据列成表:
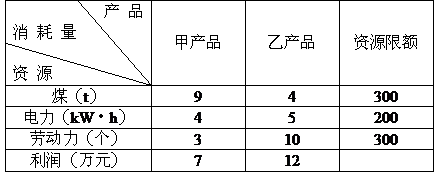
解:设每天生产甲、乙两种产品分别为x t,y t,利润总额为z万元
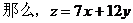
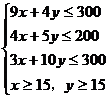
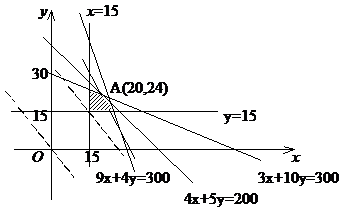
如图作出可行域,作出一组平行直线7x+12y=m(m为参数)中,经过可行域内的点且和原点距离最远的直线,此直线过4x+5y=200和3x+10y=300的交点A(20,24),即生产甲、乙两种产品分别为20t、24t时,利润总额最大,
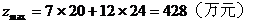
[模拟试题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com