
题目列表(包括答案和解析)
8.已知四面体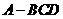 中,
中, 与
与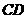 间的距离与
间的距离与
夹角分别为3与 ,则四面体
,则四面体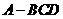 的体积为
的体积为
(A)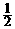 (B)1 (C)2 (D)
(B)1 (C)2 (D)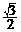
1 计算
计算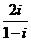 =
=
(A)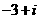 (B)
(B)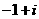 (C)
(C)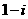 (D)
(D)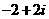
2 过点
过点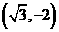 的直线
的直线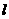 经过圆
经过圆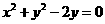 的圆心,则直线
的圆心,则直线 的倾斜角大小为
的倾斜角大小为
(A) (B)
(B) (C)
(C) (D)
(D)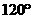
3 设函数f( x )的图象关于点(1,
设函数f( x )的图象关于点(1,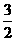 )对称,且存在反函数
)对称,且存在反函数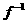 ( x ),若f(3) = 0,
( x ),若f(3) = 0,
则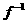 (3)等于
(3)等于
(A)-1 (B)1 (C)-2 (D)2
4 设m,n是两条不同的直线,α、β、γ是三个不同的平面
设m,n是两条不同的直线,α、β、γ是三个不同的平面 给出下列四个命题:
给出下列四个命题:
①若m⊥α,n∥α,则m⊥n; ②若α⊥γ,β⊥γ,则α∥β;
③若m∥α,n∥α,则m∥n; ④若α∥β,β∥γ,m⊥α,,则m⊥γ
其中正确命题的序号是:
(A)①和② (B)②和③ (C)③和④ (D)①和④
5.已知一个正四棱锥的各棱长均相等,则其相邻两侧面所成的二面角的大小为
(A)arcos (B)arcsin(-
(B)arcsin(-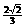 )
(C)arctan(
)
(C)arctan(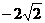 )
(D)arccot(
)
(D)arccot(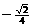 )
)
6
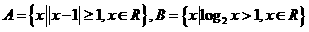 ,则“
,则“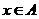 ”是“
”是“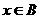 ”的
”的
(A)充分非必要条件 (B)必要非充分条件
(C)充分必要条件 (D)既非充分也非必要条件
7 若点
若点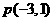 在双曲线
在双曲线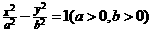 的左准线上,过点
的左准线上,过点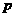 且方向向量为
且方向向量为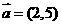 的光线,经直线
的光线,经直线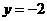 反射后通过双曲线的左焦点,则这个双曲线的离心率为
反射后通过双曲线的左焦点,则这个双曲线的离心率为
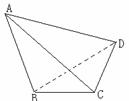 (A)
(A) (B)
(B)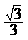 (C)
(C)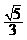 (D)
(D)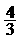
22.(本小题满分14分)
设函数f(x)=3x2+1,g(x)=2x,现有数列{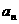 }满足条件:对于n∈
}满足条件:对于n∈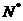 ,
, 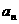 >0且f(
>0且f(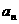 +1)-f(
+1)-f(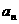 )=g(
)=g(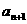 +
+ ),又设数列{
),又设数列{ }满足条件:
}满足条件: =
=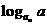 (
(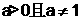 ,
,
n∈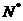 ).
).
(1)求证:数列{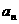 }为等比数列;
}为等比数列;
(2)求证:数列 是等差数列;
是等差数列;
(3)设k,L∈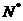 *,且k+L=5,
*,且k+L=5,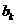 =
=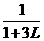 ,
,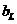 =
= ,求数列{
,求数列{ }的通项公式;
(4)如果k+L=M0(k,L∈N+,M0>3且M0是奇数),且
}的通项公式;
(4)如果k+L=M0(k,L∈N+,M0>3且M0是奇数),且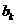 =
=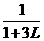 ,
,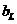 =
= ,求从第几项
,求从第几项
开始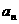 >1恒成立.
>1恒成立.
21.(本小题满分12分)
设函数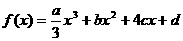 的图象关于原点对称,
的图象关于原点对称,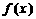 的图象在点
的图象在点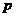 (1,
(1, )处的切线的斜率为-6,且当
)处的切线的斜率为-6,且当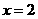 时
时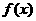 有极值.
有极值.
(1)求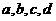 的值;
的值;
(2)若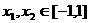 ,求证:
,求证: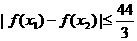 .
.
20.(本小题满分12分)
某外商到一开放区投资72万美元建起一座蔬菜加工厂,第一年各种经费12万美元,以后每年增加4万美元,每年销售蔬菜收入50万美元.设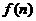 表示前n年的纯收入(
表示前n年的纯收入(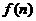 =前n年的总收入-前n前的总支出-投资额)
=前n年的总收入-前n前的总支出-投资额)
(1)从第几年开始获取纯利润?
(2)若干年后,外商为开发新项目,有两种处理方案:①年平均利润最大时以48万美元出售该厂;②纯利润总和最大时,以16万美元出售该厂,问哪种方案更合算?
19.(本小题满分12分)
设Sn是数列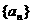 的前n项和,所有项
的前n项和,所有项 , 且
, 且 ,
,
(1)求数列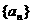 的通项公式.
的通项公式.
(2)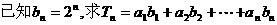 的值.
的值.
|
已知A(3,0),B(0,3),C(cos ,sin
,sin ).
).
(1)若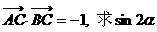 的值。
的值。
(2)O为坐标原点,若
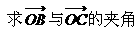 。
。
18.(本小题满分12分)
 已知函数
已知函数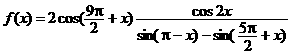
(1)求函数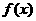 的最小正周期、
的最小正周期、
单调递减区间;
(2)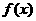 的图象由y=sinx的图
的图象由y=sinx的图
象经过怎样的变换可以得到;
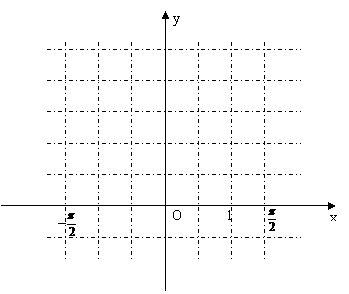
(3)在给出的直角坐标系中,画
出函数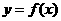 在区间
在区间
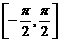 上的图象.
上的图象.
16.有穷数列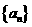 ,
, 是其前
是其前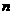 项和,定义数列的凯森和为
项和,定义数列的凯森和为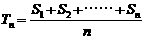 。若有99项的数列
。若有99项的数列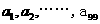 的凯森和为1000,则有100项的1,
的凯森和为1000,则有100项的1,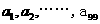 的凯森和为___________
的凯森和为___________
15.不等式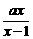 <1的解集为{x|x<1或x>2=,那么a的值为____________
<1的解集为{x|x<1或x>2=,那么a的值为____________
14.已知 ,
,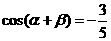 ,
,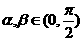 ,则
,则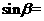
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com