
题目列表(包括答案和解析)
5.若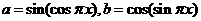 ,且
,且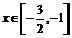 ,则 ( )
,则 ( )
A.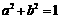 B.
B.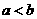 C.
C.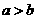 D.
D.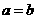
4.圆心在抛物线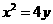 上的动圆过点(0,1),且与定直线
上的动圆过点(0,1),且与定直线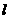 相切,则直线
相切,则直线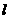 的方程为( )
的方程为( )
A.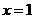 B.
B. 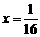 C.
C.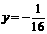 D.
D. 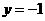
3.已知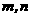 是两条不重合的直线,
是两条不重合的直线,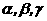 是三个两两不重合的平面,给出下列命题:
是三个两两不重合的平面,给出下列命题:
①若 ∥
∥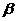 ,
,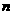 ∥
∥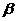 且
且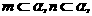 则
则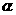 ∥
∥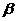 ;
;
②若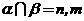 ∥
∥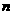 ,则
,则 ∥
∥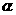 且
且 ∥
∥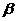 ;
;
③若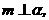
 ∥
∥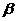 则
则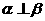 ;
;
④若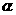 ∥
∥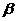 ,且
,且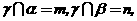 则
则 ∥
∥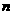 .
.
其中的正确的命题是 ( )
A.①② B.③④ C.①③ D.②④
2.复数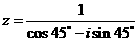 的共轭复数是 ( )
的共轭复数是 ( )
A.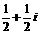 B.
B.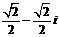 C.
C.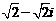 D.
D.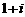
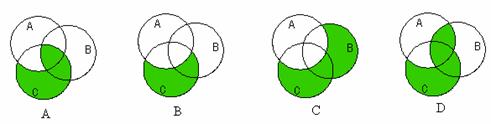
1.定义差集A-B={x|x∈A,且x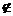 B},现有三个集合A、B、C分别用圆表示,则集合C-(A-B)可表示下列图中阴影部分的为 ( )
B},现有三个集合A、B、C分别用圆表示,则集合C-(A-B)可表示下列图中阴影部分的为 ( )
22.(12分)设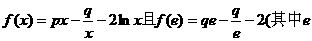 为自然对数的底数)
为自然对数的底数)
(1)求p与q的关系;
(2)若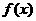 在其定义域内为单调函数,求p的取值范围;
在其定义域内为单调函数,求p的取值范围;
(3)设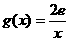 ,若在[1,e]上至少存在一点x0,使得
,若在[1,e]上至少存在一点x0,使得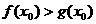 成立,求实数p的取值范围.
成立,求实数p的取值范围.
21.(12分)已知椭圆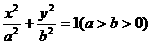 的离心率
的离心率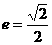 ,F1、F2为其左右焦点,点P为椭圆C上动点. △PF1F2面积的最大值为2.
,F1、F2为其左右焦点,点P为椭圆C上动点. △PF1F2面积的最大值为2.
(1)求椭圆C的方程;
(2)设椭圆C交x轴于A、B两点,M为椭圆内动点,满足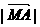 、
、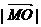 、
、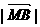 成等比数列,求
成等比数列,求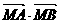 的取值范围.
的取值范围.
19.(12分)已知圆K过定点A(a,0)(a >0),圆心K在抛物线C: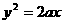 上运动,MN为圆K在y轴上截得的弦.
上运动,MN为圆K在y轴上截得的弦.
(1)求证:|MN|为定值;
(2)当|OA|是|OM|与|ON|的等差中项时,抛物线C的准线与圆K有怎样的位置关系,并说明理由.
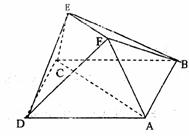 20.(12分)在如图所示的多面体中,已知正方形A BCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
20.(12分)在如图所示的多面体中,已知正方形A BCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=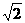 ,EF=EC=1.
,EF=EC=1.
(1)求证:平面BEF⊥平面DEF;
(2)求二面角A-BF-E的大小.
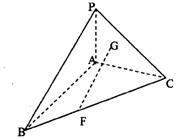 17.(10分)已知三棱锥P-ABC,PA⊥ABC,PA⊥面ABC,AB⊥AC,G为△PAC的重心,F在线段BC上,且CF=2FB.
17.(10分)已知三棱锥P-ABC,PA⊥ABC,PA⊥面ABC,AB⊥AC,G为△PAC的重心,F在线段BC上,且CF=2FB.
(1)求证FG∥面PAB.
(2)求证:FG⊥AC.
18.(12分)某电信服务点有连成一排的7座电话亭,此时全部空着,现有2位陌生人各随机选择不同的电话亭打电话.
(1)求这2个人选择的电话亭相隔数为ξ的分布列和期望;
(2)若电信管理员预言这2人之间至少相隔2座电话亭,求管理员预言为真的概率.
16.过原点引直线l与动圆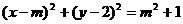 相切
相切 ,则切点M的轨迹方程为
.
,则切点M的轨迹方程为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com