
题目列表(包括答案和解析)
2. 某班共有40名学生,其中只有一对双胞胎,若从中一次随机抽查三位学生的作业,则这对双胞胎的作业同时被抽中的概率是 (结果用最简分数表示).
解析: 某班共有40名学生,其中只有一对双胞胎,若从中一次随机抽查三位学生的作业,这对双胞胎的作业同时被抽中的概率是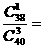
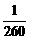

3一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在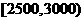 (元)/月收入段应抽出
人
(元)/月收入段应抽出
人
解析:由图知,在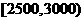 (元)/月收入段应抽出
(元)/月收入段应抽出
100×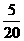 =25人
=25人
答案25
4已知甲袋中放有编号分别为0,0,1,3的四个红色小球,乙袋中放有编号为0,1,3,3,的四个黄色小球,丙袋中放有编号为1,3,3,3的四个兰色小球,现从中随机摸出红, 黄,兰色小球各一个,则摸出三个小球的编号相同的概率 ;
解析:三个小球编号相同的概率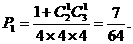
答案: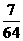
3 解答题
1. 已知A、B两地相距150千米,某人开汽车以60千米/小时的速度从A地到达B地,在B地停留1小时后再以50千米/小时的速度返回A地,把汽车离开A地的距离x表示为时间t(小时)的函数表达式是
答案: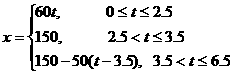
11、设15000件产品中有1000件次品,从中抽取150件进行检查,则查得次品数的数学期望为 ( )
A.15 B.10 C.20 D.5
解析:因为15000件产品中有1000件次品,从中抽取150件进行检查,则查得次品数的数学期望为150×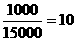
答案 B
12银行计划将某客户的资金给项目M和N投资一年,其中40%的资金给项目M,60%的资金给项目N,项目M能获得10%的年利润,项目N能获得35%的年利润。年终银行必须回笼资金,同时按一定的回报率支付给客户。为了使银行年利润不小于给M、N总投资的10%而不大于总投资的15%,则给客户的回报率最大值为 ( )
A.5% B.10% C.15% D.20%
解析:设客户投资为a,客户的回报率为x,依题意0.1a≤0.4(1+0.1)a+.06(1+0.35)a-ax≤0.15a,解得0.1≤x≤0.15,选择C。
答案 C
2 填空题
3. 一个人以6米/秒的速度去追停在交通灯前的汽车,当他离汽车25米时,交通灯由红变绿,汽车以1米/秒的加速度匀加速开走,那么 ( )
A.人可在7秒内追上汽车 B.人可在10秒内追上汽车
C.人追不上汽车,其间距离最近为5米 D.人追不上汽车,其间距离最近为7米
解析:本题是一道加速行程问题,需要运用物理知识建立数学模型,即通过加速运动建立二次函数关系式.若经t秒人刚好追上汽车,则S+25=6t,由S=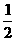 t2,得
t2,得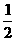 t2-6t+25=0
t2-6t+25=0 t2-12t+50=0.考虑距离差d=(S+25)-6t=
t2-12t+50=0.考虑距离差d=(S+25)-6t=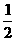 t2-6t+25=
t2-6t+25=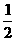 (t-6)2+7,故当t=6秒时,d有最小值7米,即人与汽车最少相距7米,故选D.
(t-6)2+7,故当t=6秒时,d有最小值7米,即人与汽车最少相距7米,故选D.
答案 D
D
4 某人从2002年1月1日起,且以后每年1月1日到银行存入a元(一年定期),若年利率r保持不变,且每年到期后存款均自动转为新一年定期,到2008年1月1日将所有存款及利息全部取回,他可取回的钱数(单位为元)为
?A.a(1+r)7 B. 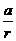 [(1+r)7-(1+r)]?C.a(1+r)8 D.
[(1+r)7-(1+r)]?C.a(1+r)8 D. 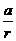 [(1+r)8-(1+r)]
[(1+r)8-(1+r)]
解析:2007年1月1日,2006年1月1日,…,2002年1月1日存入钱的本息分别为:a(1+r),a(1+r)2,…,a(1+r)6.相加即可,选择B
答案B
5停车场划出一排12个停车位置,今有8辆车需要停放,要求空车位连在一起,不同的停车方法有( )
A.A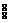 种
B.A
种
B.A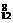 种
C.A
种
C.A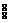 ·C
·C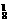 种 D.A
种 D.A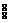 ·C
·C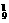 种
种
解析:插空法.空车位插入8辆车的9个空格,故有C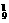 ·A
·A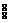 .选择.D?
.选择.D?
答案:D
6某单位有三个科室,为实现减员增效,每科室抽调2人去参加再就业培训,培训后这6人中有2人返回单位,但不回到原科室工作,且每科室至多安排一人,问共有多少种不同的安排方法( )
A.75种 B.42种 C.30种 D.15种
解析:分两类:(1)返回两人来自同一科室,返回有A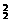 种,故有C
种,故有C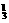 ·A
·A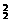 =6;(2)两人来自不同的科室,返回有2+1=3,故有(C
=6;(2)两人来自不同的科室,返回有2+1=3,故有(C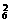 C
C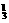 )·3=36种.共有42种. 选择B
)·3=36种.共有42种. 选择B
答案:B
7老师为研究男女同学数学学习的差异情况,对某班50名同学(其中男同学30名,女同学20名)采取分层抽样的方法,抽取一个样本容量为10的样本进行研究,某女同学甲被抽到的概率为( )
A.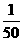 B.
B.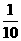 C.
C.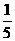 D.
D.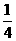
答案C
8从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有 ( )
A. 140种 B. 120种 C. 35种 D. 34种
解析:
从反面考虑,7人任意选4人的 方法数减去全选男生的 方法数即为所求
故既有男生又有女生的不同的选法共有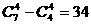 。
。
答案:D
9采用系统抽样的方法,从个体数为1003的总体中抽取一个容量为50的样本,在整个抽样过程中每个个体被抽到的概率是 ( )
A.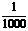 B.
B.
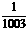 C.
C.
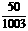 D.
D.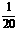
解析:抽样过程中每个个体被抽到的概率是相等的,为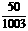
答案C
10为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图,如右,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a, b的值分别为 ( )
A.0.27,78 B.0.27,83
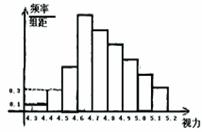
C.2.7,78 D.2.7,83
10 A解析:4.3-4.4,有1人,4.4-4.5有3人, 4.5-4.6有9人, 4.6-4.7有27人,故后六组共有87人,每组分别有27、22、17、12、7、2人, 故a= 0.27, b= 78
答案A
2. 某体育彩票规定 从01到36共36个号码中抽出7个号码为一注,每注2元. 某人想先选定吉利号18,然后再从01到17中选3个连续的号,从19到29中选2个连续的号,从30到36中选1个号组成一注,则此人把这种要求的号买全,至少要花( )
从01到36共36个号码中抽出7个号码为一注,每注2元. 某人想先选定吉利号18,然后再从01到17中选3个连续的号,从19到29中选2个连续的号,从30到36中选1个号组成一注,则此人把这种要求的号买全,至少要花( )
A. 1050元 B. 1052元 C. 2100元 D. 2102元
解析 从01到17中选连续3个号有15种方法,从19到29中选连续2个号有10种选法,从30到36中选1个有7种选法,故购买注数为1050注至少花1050×2=2100元.
从01到17中选连续3个号有15种方法,从19到29中选连续2个号有10种选法,从30到36中选1个有7种选法,故购买注数为1050注至少花1050×2=2100元.
答案 C
C
1 选择题
1. 某商场对顾客实行购物优惠活动,规定一次购物付款总额 ①如果不超过200元,则不予优惠,②如果超过200元但不超过500元,则按标价给予9折优惠,③如果超过500元,其500元按②条给予优惠,超过500元的部分给予7折优惠。某人两次去购物,分别付款168元和423元,假设他一次购买上述同样的商品,则应付款( )
①如果不超过200元,则不予优惠,②如果超过200元但不超过500元,则按标价给予9折优惠,③如果超过500元,其500元按②条给予优惠,超过500元的部分给予7折优惠。某人两次去购物,分别付款168元和423元,假设他一次购买上述同样的商品,则应付款( )
A 413.7元 B 513.7元 C 546.6元 D 548.7元
解析 此人购买的商品原价为168+423÷90%=638元,若一次购买同样商品应付款为500×90%+(638–500)×70%=450+96.5=546.6元
此人购买的商品原价为168+423÷90%=638元,若一次购买同样商品应付款为500×90%+(638–500)×70%=450+96.5=546.6元
答案 C
C
(二)2008年高考预测
通过对2007年高考试题及考纲分析,笔者认为.08年高考应用题试题数量会保持稳定,一般为两小一大。在小题中考查函数、数列、不等式、排列组合、概率等知识的应用,解答题仍会以概率统计为基本题型进行考察。因此要加强以下几方面训练。
1.函数、数列、不等式应用题、排列组合问题以选择填空为主。
2概率与统计问题训练以解答题为主。
20.(14分)已知点P在曲线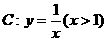 上,曲线C在点P处的切线与函数
上,曲线C在点P处的切线与函数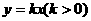 的图象交于点A,与
的图象交于点A,与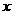 轴交于点B,设点P的横坐标为
轴交于点B,设点P的横坐标为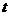 ,点A,B的横坐标分别为
,点A,B的横坐标分别为 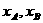 ,记
,记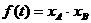
Ⅰ)求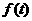 的解析式
的解析式
Ⅱ)设数列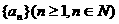 满足
满足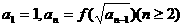 ,求数列
,求数列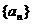 的通项公式
的通项公式
Ⅲ)在Ⅱ)的条件下,当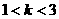 时,证明不等式
时,证明不等式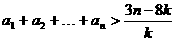
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com