
题目列表(包括答案和解析)
19.(本小题满分16分)
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交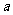 元(
元(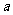 为常数,2≤a≤5 )的税收.设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与
为常数,2≤a≤5 )的税收.设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与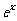 (e为自然对数的底数)成反比例.已知每件产品的日售价为40元时,日销售量为10件。
(e为自然对数的底数)成反比例.已知每件产品的日售价为40元时,日销售量为10件。
(Ⅰ)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(Ⅱ)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值。
18.(本小题满分15分)
已知直线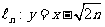 与圆
与圆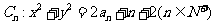 交于不同点An、Bn,其中数列
交于不同点An、Bn,其中数列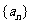 满足:
满足: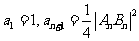 .
.
(Ⅰ)求数列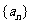 的通项公式;
的通项公式;
(Ⅱ)设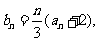 求数列
求数列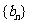 的前n项和
的前n项和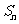 .
.
17.(本小题满分15分)
如图,已知椭圆C: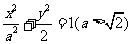 的左右焦点分别为F1、F2,点B为椭圆与y轴的正半轴的交点,点P在第一象限内且在椭圆上,且PF2与x轴垂直,
的左右焦点分别为F1、F2,点B为椭圆与y轴的正半轴的交点,点P在第一象限内且在椭圆上,且PF2与x轴垂直,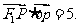
(Ⅰ)求椭圆C的方程;
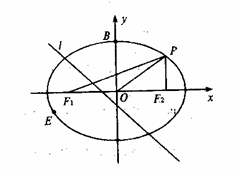 (Ⅱ)设点B关于直线
(Ⅱ)设点B关于直线 的对称点E(异于点B)在椭圆C上,求m的值。
的对称点E(异于点B)在椭圆C上,求m的值。
16.(本小题满分14分)
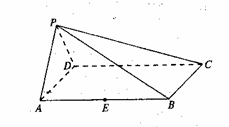
如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧面PAD⊥底面ABCD,PA=PD,且PD与底面ABCD所成的角为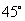 ,
,
(Ⅰ)求证:PA⊥平面PDC;
(Ⅱ)已知E为棱AB的中点,问在棱PD上是否存在一点Q,使EQ∥平面PBC?若存在,写出点Q的位置,并证明你的结论;若不存在,说明理由。
15.(本小题满分14分)
在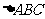 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为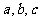 ,已知向量
,已知向量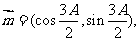
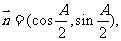 且满足
且满足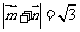 ,
,
(Ⅰ)求角A的大小;
(Ⅱ)若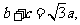 试判断
试判断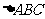 的形状。
的形状。
22.数列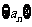 满足递推式
满足递推式 ,其中
,其中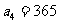 ,
,
(1)求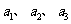 ;
;
(2)若存在一个实数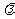 ,使得
,使得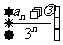 为等差数列,求
为等差数列,求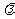 值;
值;
(3)(理)求数列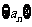 的前
的前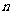 项之和。
项之和。
21. 如图,椭圆
如图,椭圆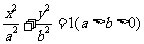 与过点
与过点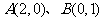 的直线有且只有一个公共点
的直线有且只有一个公共点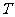 ,且椭圆的离心率
,且椭圆的离心率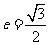
(1)求椭圆的方程;
(2)设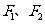 分别为椭圆的左、右焦点,
分别为椭圆的左、右焦点,
求证: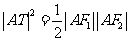 。
。
20.(理)已知函数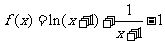 ,
,
(1)求函数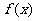 的单调递增区间;
的单调递增区间;
(2)若 ,证明:
,证明: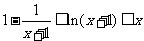 。
。
(文)已知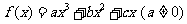 在
在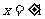 取得极值,且
取得极值,且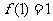 ,
,
(1)试求常数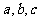 的值;
的值;
(2)试判断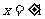 是函数的极大值还是极小值,并说明理由。
是函数的极大值还是极小值,并说明理由。
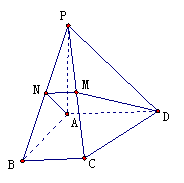
19.如图,在四棱椎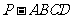 中,底面为直角梯形,且
中,底面为直角梯形,且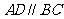 ,
,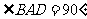 ,
, ,且
,且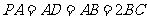 ,
,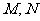 分别为
分别为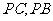 的中点。
的中点。
(1)求证: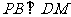 ;
;
 (2)求
(2)求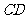 与平面
与平面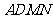 所成的角。
所成的角。
18.已知函数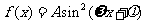 ,
,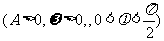 ,且
,且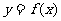 的最大值为
的最大值为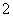 ,其图象相邻两对称轴间的距离为
,其图象相邻两对称轴间的距离为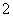 ,并过点
,并过点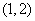 ,
,
(1)求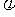 ;
;
(2)计算 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com