
题目列表(包括答案和解析)
4.若函数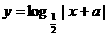 的图像不经过第二象限,则a的取值范围是( )
的图像不经过第二象限,则a的取值范围是( )
A.(0,+∞) B.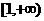 C.(-∞,0) D.
C.(-∞,0) D.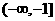
3.经过圆x2+2x+y2=0的圆心G,且与直线y=x垂直的直线方程是( )
A.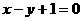 B.
B.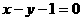
C.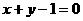 D.
D.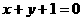
2.设集合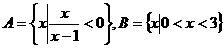 ,那么“
,那么“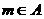 ”是“
”是“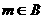 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
1.设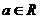 ,且
,且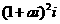 为正实数,则
为正实数,则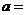 ( )
( )
A. B.
B.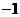 C.
C.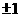 D.
D.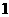
22. (本题满分14分)已知数列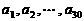 ,其中
,其中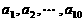 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;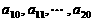 是公差为
是公差为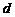 的等差数列;
的等差数列;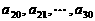 是公差为
是公差为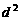 的等差数列(
的等差数列(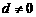 ).
).
(1)若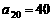 ,求
,求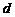 ;
;
(2)试写出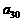 关于
关于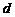 的关系式,并求
的关系式,并求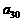 的取值范围;
的取值范围;
(3)续写已知数列,使得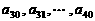 是公差为
是公差为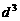 的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
的等差数列,……,依次类推,把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例),并进行研究,你能得到什么样的结论?
20. (本题满分12分)函数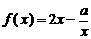 的定义域为
的定义域为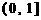 (
(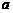 为实数).
为实数).
(1) 当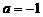 时,求函数
时,求函数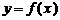 的值域;(2) 判断函数
的值域;(2) 判断函数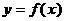 的单调性(不必证明);
的单调性(不必证明);
(3) 若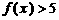 在
在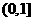 上恒成立,求
上恒成立,求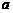 的取值范围.
的取值范围.
21(本题满分12分)设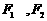 分别是椭圆C:
分别是椭圆C: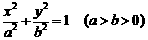 的左右焦点
的左右焦点
(1)设椭圆C上的点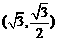 到
到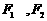 两点距离之和等于4,写出椭圆C的方程和焦点坐标
两点距离之和等于4,写出椭圆C的方程和焦点坐标
(2)设K是(1)中所得椭圆上的动点,求线段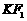 的中点B的轨迹方程
的中点B的轨迹方程
(3)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为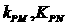 试探究
试探究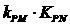 的值是否与点P及直线L有关,不必证明你的结论。
的值是否与点P及直线L有关,不必证明你的结论。
19. (本题满分12分)已知向量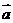 =(−cosx
, sinx),
=(−cosx
, sinx),
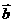 =(cosx
,
=(cosx
,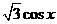 ),函数f(x)=
),函数f(x)=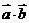
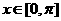
(1)求函数f(x)的最大值
(2)当函数f(x)取得最大值时,求向量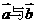 夹角的大小.
夹角的大小.
|
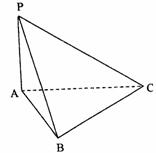
18.(本题满分12分)如图,三棱锥P-ABC的底面ABC是一个正三角形,PA=AB=a,且PA⊥底面ABC。
(1)试求三棱锥C-PAB的体积;
(2)(文) PC与AB所成角的大小(用反三角函数值表示)。
(理)试求PC与平面PAB所成角的大小(用反三角函数值表示)。
17.(本题满分12分)
(文)对某型号1000只灯泡的使用寿命(单位:小时)统计如下表所示:
|
寿命分组 |
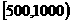 |
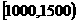 |
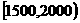 |
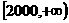 |
|
灯泡个数 |
172 |
428 |
392 |
71 |
(1)从这1000只灯泡中任选1只,求该灯泡寿命不足1500小时的概率;
(2)从这1000只灯泡中任选3只灯泡,求至多有2只灯泡寿命不足1500小时的概率。
(理)甲,乙两人射击,每次射击击中目标的概率分别是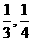 . 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.
. 现两人玩射击游戏,规则如下:若某人某次射击击中目标,则由他继续射击,否则由对方接替射击. 甲、乙两人共射击3次,且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.
(1) 求3次射击的人依次是甲、甲、乙,且乙射击未击中目标的概率;
 (2) 求乙至少有1次射击击中目标的概率.
(2) 求乙至少有1次射击击中目标的概率.
16.在ΔABC中,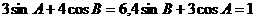 ,则C等于( )
,则C等于( )
A.300 B.1500 C.300或1500 D.600或1200
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com