
题目列表(包括答案和解析)
7.直线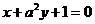 与直线
与直线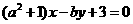 互相垂直,
互相垂直,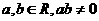 ,则
,则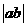 的最小值为
的最小值为
6. 某单位购买6张北京奥运会某场比赛门票,其中有2张甲票,其余为乙票,三名职工从中各抽一张,至少有一人抽到甲票的抽法为
A 4 B 16 C 12 D 8
5.设函数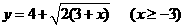 ,则它的反函数为
,则它的反函数为
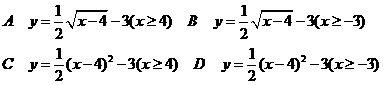
4.已知定点A,B,且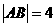 ,动点P满足
,动点P满足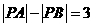 ,则
,则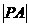 的最小值为
的最小值为
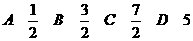
3.函数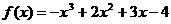 在点(2 , 2)处的切线的倾斜角为
在点(2 , 2)处的切线的倾斜角为
A. 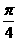 B.
B. 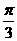 C.
C.
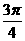 D.
D.
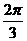
2.函数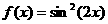 的最小正周期是
的最小正周期是
A.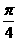 B.
B.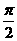 C.
C.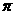 D.
D.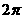
1.设集合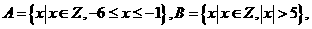 则
则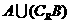 中元素个数为
中元素个数为

21.(本小题满分14分)
(Ⅰ)解:当a=1时,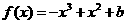 ,
,
因为f(-1)=b+2>b,
所以,函数f (x)的图象不能总在直线y=b的下方. 4分
(Ⅱ)解:由题意,得f '(x)=-3x2+2ax,
令f′(x)=0,解得x=0或x=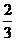 a,
5分
a,
5分
当a<0时,由f′(x)>0,解得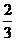 a<x<0,
a<x<0,
所以f (x)在(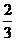 a,0)上是增函数,与题意不符,舍去;
a,0)上是增函数,与题意不符,舍去;
当a=0时,由f′(x)=-3x2≤0,与题意不符,舍去; 6分
当a>0时,由f' (x)>0,解得0<x<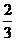 a, 所以f (x)在(0,
a, 所以f (x)在(0,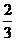 a)上是增函数,
a)上是增函数,
又f (x)在(0,2)上是增函数, 所以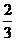 a≥2,解得a≥3,
a≥2,解得a≥3,
综上,a的取值范围为[3,+∞). 9分
(Ⅲ)解:因为方程f (x)=-x3+ax2+b=0最多只有3个根,由题意,在区间(-1,0)内仅有一根, 所以f (-1)·f (0)=b(1+a+b)<0, ①
同理f (0)·f (1)=b(-1+a+b)<0, ② 11分
当b>0时,由①得1+a+b<0,即a<-b-1,
由②得-1+a+b<0,即a<-b+1,
因为-b-1<- b +1,所以a<- b -1<-1,即a<-1;
当b <0时, 由①得1+a+ b >0,即a>- b -1,
由②得-1+a+ b >0,即a >- b +1,
因为- b -1<- b +1,所以a >- b +1>1, 即a >1;
当b =0时,因为f(0)=0,所以f(x)=0有一根0,这与题意不符.
综上,│a│>1. 14分
注:在第(Ⅲ)问中,得到①②后,可以在坐标平面aOb内,用线性规划方法解.请相应评分.
20.(本小题满分13分)
(Ⅰ)解:设A(x1,y1),
因为P为AM的中点,且P的纵坐标为O,M的纵坐标为1,
所以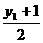 =0,解得y1=-1,
1分
=0,解得y1=-1,
1分
又因为点A(x1,y1)在椭圆C上,所以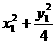 =1,即
=1,即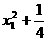 =1,解得x1=±
=1,解得x1=±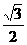 ,
,
则点A的坐标为(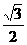 ,1)或(-
,1)或(-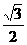 ,-1),
3分
,-1),
3分
所以直线l的方程为4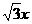 -3y+3=0,或4
-3y+3=0,或4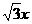 +3y-3=0. 6分
+3y-3=0. 6分
(Ⅱ)设A(x1,y1),B(x2,y2),则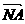 =(x1,y1-
=(x1,y1-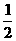 ),
),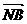 =(x2,y2-
=(x2,y2-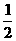 ),
),
所以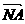 +
+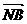 =(x1+x2,y1+y2-1),
=(x1+x2,y1+y2-1),
则|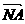 +
+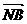 │=
│=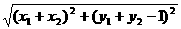 , 8分
, 8分
当直线AB的斜率不存在时,其方程为x=0,
A(0,2),B(0,-2),此时│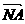 +
+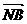 │=1;
9分
│=1;
9分
当直线AB的斜率存在时,设其方程为y=kx+1,
由题设可得A、B的坐标是方程组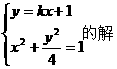 ,
,
消去y得(4+k2)x2+2kx-3=0,所以Δ=(2k)2+12(4+k2)>0,x1+x2=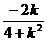 ,
,
则y1+y2=(kx1+1)+(kx2+1)=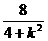 ,
10分
,
10分
所以│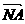 +
+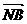 │2=(
│2=(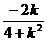 )2+(
)2+(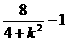 )2=
)2=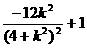 ≤1,
≤1,
当k=0时,等号成立,即此时│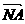 +
+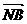 │取得最大值1.
12分
│取得最大值1.
12分
综上,当直线AB的方程为x=0或y=1时,│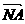 +
+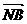 │有最大值1. 13分
│有最大值1. 13分
19.(本小题满分12分)
(Ⅰ)解:因为Sn=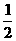 nan+an-c,
nan+an-c,
所以当n=1时,S1=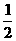 a1+a1-c,解得a1=2c,
2分
a1+a1-c,解得a1=2c,
2分
当n=2时,S2=a2+a2-c,即a1+a2=2a2-c,解得a2=3c,
所以3c=6,解得c=2; 4分
则a1=4,数列{an}的公差d=a2-a1=2,
所以an=al+(n-1)d=2n+2. 6分
(Ⅱ);因为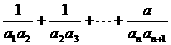
=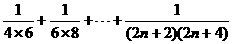 7分
7分
=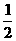 (
(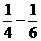 )+
)+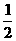 (
(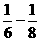 )+…+1
)+…+1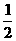 (
(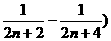 8分
8分
=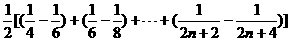
=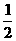 (
(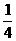
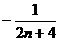 )
)
=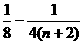 . 10分
. 10分
因为n∈N*, 所以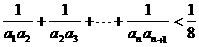 . 12分
. 12分
注:为降低难度,此题故意给出多余条件,有多种解法,请相应评分.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com