
题目列表(包括答案和解析)
5.设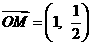 ,
,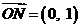 ,则满足条件
,则满足条件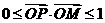 ,
,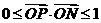 的动点
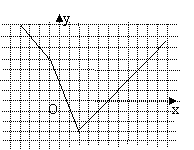
的动点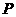 的变化范围(图中阴影部分含边界)是( )
的变化范围(图中阴影部分含边界)是( )
4.已知圆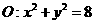 ,点
,点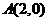 ,动点
,动点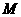 在圆上,则
在圆上,则 的最大值为( )
的最大值为( )
A.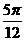 B.
B.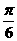 C.
C.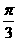 D.
D. 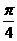
3.已知 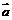 ,
,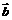 是两个非零向量,给定命题p: |
是两个非零向量,给定命题p: |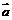 ·
·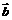 |=|
|=|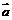 ||
||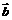 |,命题q:
|,命题q: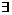 t∈R,使得
t∈R,使得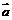 =t
=t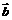 ,则p是q的( )
,则p是q的( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2.设集合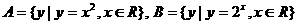 ,则
,则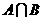 等于( )
等于( )
A.{2,4} B.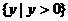 C.{(2,4),(4,16)} D.{4,16}
C.{(2,4),(4,16)} D.{4,16}
1.已知复数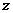 满足
满足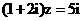 ,则
,则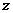 等于( )
等于( )
A.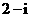 B.
B.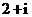 C.
C.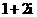 D.
D.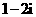
21.本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.
(1)(本小题满分7分)选修4-2:矩阵与变换
解:(I)设矩阵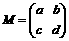
∴ 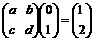 且
且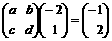 ,即
,即 且
且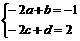
∴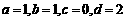
∴矩阵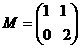
(II) ∵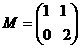 , ∴矩阵M的特征矩阵为
, ∴矩阵M的特征矩阵为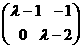
∴矩阵M的特征方程为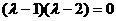
 ∴矩阵M的特征值为1和2
∴矩阵M的特征值为1和2
(2)(本小题满分7分)选修4-4:坐标系与参数方程
解:圆 与圆
与圆 公共弦的长度为
公共弦的长度为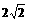
(3)(本小题满分7分)选修4-5:不等式选讲
解:(I)∵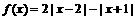
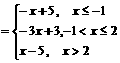
∴函数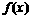 的图象如图所示,且其单调递增区间为
的图象如图所示,且其单调递增区间为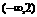 ,单调递减区间为
,单调递减区间为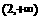
(II)∵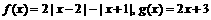
∴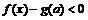 即为
即为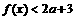
∴为使关于 的不等式
的不等式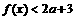 有解,当且仅当
有解,当且仅当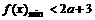
由(I)知
∴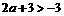 ,即得
,即得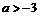
∴实数 的取值范围是
的取值范围是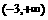
本资料由《七彩教育网》 提供!
20.(本小题满分14分)
解:(1)∵ , ∴
, ∴
要使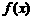 在区间
在区间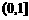 上是增函数,当且仅当
上是增函数,当且仅当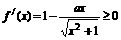 在
在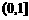 上恒成立
上恒成立
即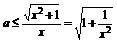 在
在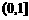 上恒成立,即
上恒成立,即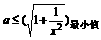
∵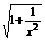 在
在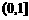 上单调递减,∴
上单调递减,∴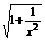 在
在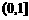 上的最小值是
上的最小值是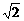
∴ 的取值范围是
的取值范围是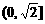
(2)由(1)可知,当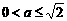 时,
时,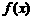 在
在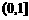 上是增函数
上是增函数
此时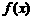 在
在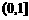 上的最大值是
上的最大值是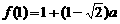
当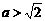 时,令
时,令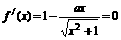 ,解得
,解得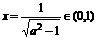
∵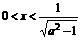 时
时 ,
,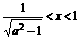 时
时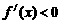
∴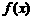 在
在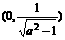 上单调递增,在
上单调递增,在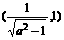 上单调递减
上单调递减
此时,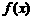 在
在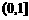 上的最大值是
上的最大值是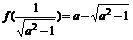
综上所述,当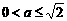 时,
时,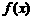 在区间
在区间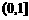 上的最大值是
上的最大值是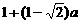 ;当
;当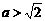 时,
时,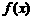 在区间
在区间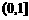 上的最大值是
上的最大值是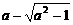
(3)∵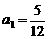 ,
,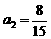 ,
,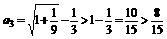
∴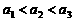
当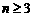 时,设
时,设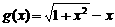
∴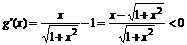 ,∴
,∴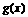 在
在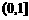 上单调递减
上单调递减
令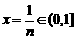 ,则
,则
∴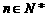 时有
时有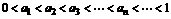
∵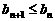 ,即
,即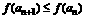 ,由(2)知
,由(2)知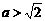
要使 取到最小值必须
取到最小值必须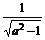 尽可能的大。
尽可能的大。
由(2)知只须满足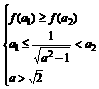 即
即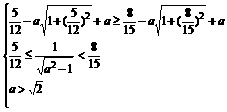
解得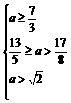 ∴
∴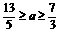 , ∴
, ∴ 的最小值为
的最小值为
19.(本小题满分13分)
解:(1)∵ ,∴
,∴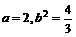
∴椭圆 的方程为
的方程为 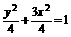
(2)∵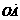 ·
·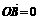 ,∴
,∴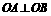
由对称性知
∴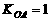 ,∴直线
,∴直线 的方程为
的方程为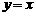
由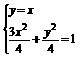 得
得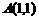
∵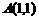 在圆
在圆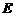 :
: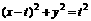 上
上
∴ ,∴
,∴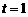
(3)∵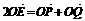 ,
,
∴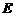 是
是 的中点,即
的中点,即 、
、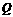 是圆
是圆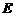 直径的两个端点,∴
直径的两个端点,∴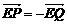
∴ ·
·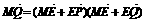
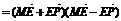
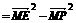
∵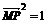 ,∴
,∴ ·
·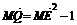
设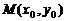 ,则
,则
∴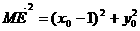
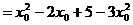
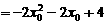
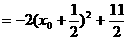
∵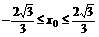 ,∴
,∴ 时,
时,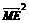 取到最大值
取到最大值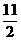
∴ ·
·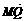 的最大值为
的最大值为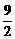
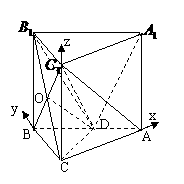
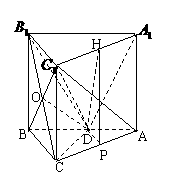
18.(本小题满分13分)
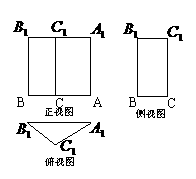 (1)证明:连结
(1)证明:连结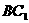 交
交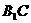 于O,连结OD,
于O,连结OD,
在 中,点O和D都是中点
中,点O和D都是中点
∴OD||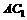 ,又
,又
∴
解:(2)∵BC、AC、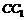 两两垂直
两两垂直
∴以C为原点建立空间直角坐标系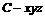
∵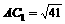 ,
,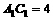 ,∴
,∴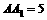
∴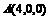 ,
,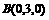 ,
,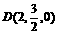 ,
, ,
,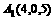
∴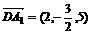 ,
,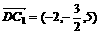 ,
,
设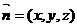 为平面
为平面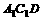 的法向量,则
的法向量,则
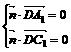 ,即
,即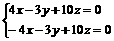
取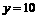 ,得
,得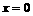 ,
,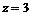 ,即解得
,即解得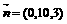
 设点A到平面
设点A到平面 的距离为
的距离为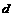 ,则
,则 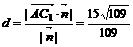
∴点A到平面 的距离为
的距离为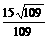 。
。
(3)设二面角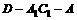 的二面角为
的二面角为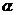 ,则
,则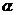 为锐角
为锐角
又由(2)知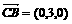 为平面
为平面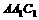 的法向量
的法向量
∴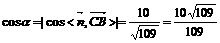
∴二面角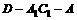 的余弦值为
的余弦值为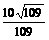
 另解:设点P点AC中点,H为
另解:设点P点AC中点,H为 中点,连结DP,PH,DH
中点,连结DP,PH,DH
∴PD||BC,又
∴ ,又
,又
∴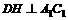
∴ 为二面角
为二面角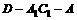 的平面角,且
的平面角,且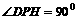
∵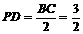 ,
,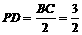
∴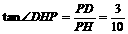 ,∴
,∴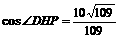
∴二面角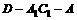 的余弦值为
的余弦值为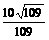
17.(本小题满分13分)
解:①不采取预防措施时,总费用为500×0.3=150(万元);
②若单独采取甲措施,则预防费用为60万元,发生突发事件的概率为0.1,损失期望值为500×0.1=50(万元),所以总费用为60+50=110(万元);
③若单独采取乙措施,则预防费用为42万元,发生突发事件的概率为0.15,损失期望值为500×0.15=75(万元),所以总费用为42+75=117(万元);
④若联合采取甲、乙两种措施,则预防费用为60+42=102万元,发生突发事件的概率为0.1×0.15=0.015,损失期望值为500×0.015=7.5(万元),所以总费用为102+7.5=109.5(万元);
综合①②③④知,应选择联合采用甲、乙两种措施可以使总费用最少。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com