21.(18')数列{a_n}满足a₁=2, a_n+1=λa_n+2ⁿ (n∈N^*), λ为非零常数

⑴是否存在实数λ,使得数列{a_n}成为等差数列或者成为等比数列.

若存在则找出所有的λ,并求出对应的通项公式;若不存在则说明理由

⑵当λ=11时,记b_n= a_n+×2ⁿ,证明数列{b_n}是等比数列

20.(18')⑴证明命题: 若直线l过抛物线y²=2px (p>0)的焦点F(,0),交抛物线于AB两点,O为坐标原点,

那么·=-p²

⑵写出第⑴题中命题的逆命题.如其为真,则给出证明; 如其为假,则说明理由

⑶把第⑴题中命题作推广,使其是你推广的特例,并对你的推广作出证明

19.(14')已知函数f (x)=

⑴判断f (x)在区间(0,+∞)上的单调性,并证明

⑵若关于x的方程f (x)=k有根在[2,3]内,求实数k的取值范围

⑶若关于x的方程f (x)=k x²有四个不同的实数根,求实数k的取值范围

18.(12')袋中有形状、质地都相同的黑球、白球和红球共10只,已知从袋中任意摸出一个球,得到黑球的概率

为,从袋中任意摸出两个球,至少得到一个白球的概率为

求⑴从袋中任意摸出两个球,至少得到一个黑球的概率

⑵袋中白球的个数

理⑶从袋中任意摸出三个球,记得到白球的个数为ξ,写出随机变量ξ的分布列,并求其数学期望Eξ

17.(12')直三棱柱ABC-A₁B₁C₁中的底面是等腰直角△,AB=AC=2,∠BAC=90°,棱AA₁=3,若D是BC中点

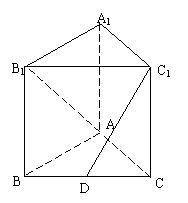理⑴求证:AD⊥平面BCC₁B₁)

⑵求异面直线DC₁与AB₁所成角的大小

16.设等差数列{a_n}的前n项和为S_n,且S₁₅>0, S₁₆<0,则, ,..., 中最大的是(　 )

A.　　　 　　B.　 　　　C. 　 　 　　　D.

15. a≠b且a ²sinθ+acosθ-2=0,b²sinθ+bcosθ-2=0,则连接(a ,a ²)、(a ,a ²)两点的直线与圆x²+y²=1的关系

为(　 )

A.相交　　 　 B. 相离　 　　C.相切　 　 D.以上均有可能

14. a>0, b>0, a,b的等差中项是, x=a+, y=b+,则x+y的最小值是(　 )

A.6　　　　 　 B． 5　　　　 C.4 　　 　　　　D.3

13.向量(a,(b,(c满足(a+(b+(c=(0,(a⊥(b,|(a|=1,|(b|=2,则|(c|等于(　 )

A.1　 　　　B.　　 　　　C.2 　　　　D．

12.定义:区间[a,b]( a<b)的长度为b-a.已知函数y=|log_0.5 x|的定义域为[a,b],值域为[0,2],

则区间[a,b]长度的最大值是