
题目列表(包括答案和解析)
67. 从点O引射线OA、OB、OC,若∠AOB=∠AOC,则A在平面BOC的射影在∠BOC平分线上;若A到OB与OC距离相等,则A在平面BOC的射影在∠BOC平分线上;
66. 平面图形翻折(展开):注意翻折(展开)后在同一平面图形中角度、长度不变;
65. 求球面两点A、B距离①求|AB|②算球心角∠AOB弧度数③用公式L球面距离=θ球心角×R;纬线半径r=Rcos纬度。S球=4πR2;V球=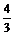 πR3;
πR3;
64. 空间距离:①异面直线间距离:找公垂线; ②平行线与面间距离(两平行面间距离)→点到面距离:直接法、等体积、转移法、垂面法、向量法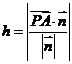 .③点到线距离:用三垂线定理作垂线后再求;
.③点到线距离:用三垂线定理作垂线后再求;
63. 平行六面体→直平行六面体→长方体→正四棱柱→正方体间联系
三棱锥中:侧棱长相等(侧棱与底面所成角相等)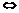 顶点在底面射影为底面外心;侧棱两两垂直(两对对棱垂直)
顶点在底面射影为底面外心;侧棱两两垂直(两对对棱垂直)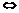 顶点在底面射影为底面垂心;斜高相等(侧面与底面所成相等)
顶点在底面射影为底面垂心;斜高相等(侧面与底面所成相等) 顶点在底面射影为底面内心;正棱锥各侧面与底面所成角相等为θ,则S侧cosθ=S底;正三角形四心?内切外接圆半径?;
顶点在底面射影为底面内心;正棱锥各侧面与底面所成角相等为θ,则S侧cosθ=S底;正三角形四心?内切外接圆半径?;
62. 求空间角①异面直线所成角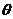 的求法:(1)范围:
的求法:(1)范围: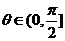 ;(2)求法:平移以及补形法、向量法。如(1)正四棱锥
;(2)求法:平移以及补形法、向量法。如(1)正四棱锥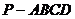 的所有棱长相等,
的所有棱长相等,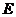 是
是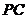 的中点,那么异面直线
的中点,那么异面直线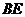 与
与 所成的角的余弦值等于____(答:
所成的角的余弦值等于____(答: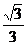 );(2)在正方体AC1中,M是侧棱DD1的中点,O是底面ABCD的中心,P是棱A1B1上的一点,则OP与AM所成的角的大小为____(答:90°);②直线和平面所成的角:(1)范围
);(2)在正方体AC1中,M是侧棱DD1的中点,O是底面ABCD的中心,P是棱A1B1上的一点,则OP与AM所成的角的大小为____(答:90°);②直线和平面所成的角:(1)范围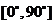 ;(2)斜线与平面中所有直线所成角中最小的角。:(3)求法:作垂线找射影或求点线距离 (向量法);如(1)在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,BD=1,则AD与平面AA1C1C所成的角为______(答:arcsin
;(2)斜线与平面中所有直线所成角中最小的角。:(3)求法:作垂线找射影或求点线距离 (向量法);如(1)在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,BD=1,则AD与平面AA1C1C所成的角为______(答:arcsin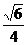 );(2)正方体ABCD-A1B1C1D1中,E、F分别是AB、C1D1的中点,则棱 A1B1 与截面A1ECF所成的角的余弦值是______(答:
);(2)正方体ABCD-A1B1C1D1中,E、F分别是AB、C1D1的中点,则棱 A1B1 与截面A1ECF所成的角的余弦值是______(答: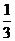 );③二面角:二面角的求法:定义法、三垂线法、垂面法、面积射影法:
);③二面角:二面角的求法:定义法、三垂线法、垂面法、面积射影法: 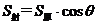 、转化为法向量的夹角。如(1)正方形ABCD-A1B1C1D1中,二面角B-A1C-A的大小为________(答:
、转化为法向量的夹角。如(1)正方形ABCD-A1B1C1D1中,二面角B-A1C-A的大小为________(答: );(2)正四棱柱ABCD-A1B1C1D1中对角线BD1=8,BD1与侧面B1BCC1所成的为30°,则二面角C1-BD1-B1的大小为______(答:
);(2)正四棱柱ABCD-A1B1C1D1中对角线BD1=8,BD1与侧面B1BCC1所成的为30°,则二面角C1-BD1-B1的大小为______(答: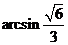 );(3)从点P出发引三条射线PA、PB、PC,每两条的夹角都是60°,则二面角B-PA-C的余弦值是______(答:
);(3)从点P出发引三条射线PA、PB、PC,每两条的夹角都是60°,则二面角B-PA-C的余弦值是______(答: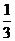 );
);
61. 常用定理:①线面平行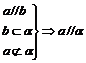 ;
;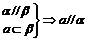 ;
;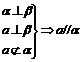
②线线平行: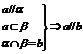 ;
;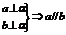 ;
;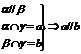 ;
;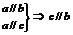
③面面平行: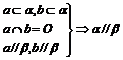 ;
;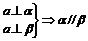 ;
;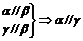
④线线垂直: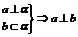 ;所成角900;
;所成角900;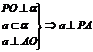 (三垂线);逆定理?
(三垂线);逆定理?
⑤线面垂直: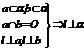 ;
;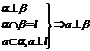 ;
;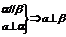 ;
;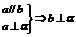
⑥面面垂直:二面角900; 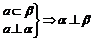 ;
;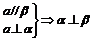
60. 位置和符号①空间两直线:平行、相交、异面;判定异面直线用定义或反证法②直线与平面: a∥α、a∩α=A (a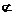 α) 、a
α) 、a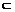 α③平面与平面:α∥β、α∩β=a
α③平面与平面:α∥β、α∩β=a
59、分式、高次不等式:通分因式分解后用根轴法(穿线法).注意偶次式与奇次式符号.奇穿偶回
如(1)解不等式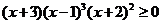 。(答:
。(答: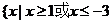 或
或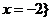 );(2)解不等式
);(2)解不等式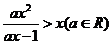 (答:
(答: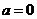 时,
时,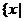
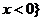 ;
;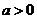 时,
时,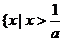 或
或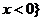 ;
;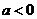 时,
时,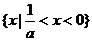 或
或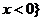 )
)
58、解绝对值不等式:①几何法(图像法)②定义法(零点分段法);③两边平方
④公式法:|f(x)|>g(x)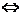 ;|f(x)|<g(x)
;|f(x)|<g(x)  。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com