
题目列表(包括答案和解析)
4.i是虚数单位,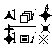 等于
等于
A.i B.-i C.1 D.-1
3.若一个底面是正三角形的三棱柱的正规视图如图所示,则其侧面积等于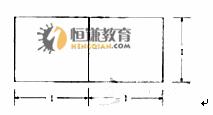
A.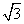 B.2
C.
B.2
C.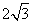 D.6
D.6
2.计算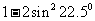 的结果等于
的结果等于
A.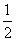 B.
B.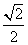 C.
C.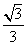 D.
D.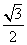
1.若集合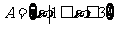 ,
,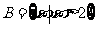 ,则
,则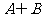 等于
等于
A.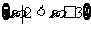 B.
B.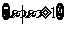 C.
C.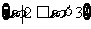 D.
D.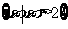
21、(本小题满分14分)
已知函数f(x)=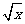 ,g(x)=alnx,a
,g(x)=alnx,a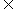 R。
R。
(Ⅰ)若曲线y=f(x)与曲线y=g(x)相交,且在交点处有相同的切线,求a的值及该切线的方程;
(Ⅱ)设函数h(x)=f(x)-
g(x),当h(x)存在最小之时,求其最小值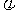 (a)的解析式;
(a)的解析式;
(Ⅲ)对(2)中的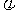 (a)和任意的
(a)和任意的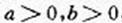 ,证明:
,证明:
解 (Ⅰ)f’(x)=
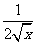 ,g’(x)=
,g’(x)=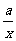 (x>0),
(x>0),
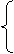 由已知得
由已知得 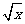 =alnx,
=alnx,
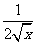 =
=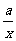 , 解德a=
, 解德a=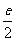 ,x=e2,
,x=e2,
 两条曲线交点的坐标为(e2,e) 切线的斜率为k=f’(e2)=
两条曲线交点的坐标为(e2,e) 切线的斜率为k=f’(e2)= 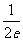 ,
,
 切线的方程为y-e=
切线的方程为y-e=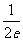 (x- e2).
(x- e2).
(Ⅱ)由条件知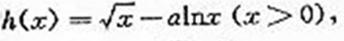
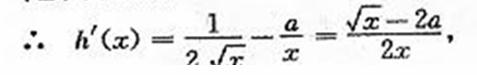
(1)
当a.>0时,令h  (x)=0,解得x=
(x)=0,解得x=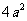 ,
,
所以当0 <
x< 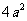 时 h
时 h  (x)<0,h(x)在(0,
(x)<0,h(x)在(0,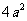 )上递减;
)上递减;
当x>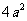 时,h
时,h  (x)>0,h(x)在(0,
(x)>0,h(x)在(0,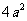 )上递增。
)上递增。
所以x>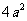 是h(x)在(0, +∞ )上的唯一极致点,且是极小值点,从而也是h(x)的最小值点。
是h(x)在(0, +∞ )上的唯一极致点,且是极小值点,从而也是h(x)的最小值点。
所以Φ (a)=h(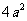 )= 2a-aln
)= 2a-aln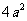 =2
=2
(2)当a ≤ 0时,h(x)=(1/2-2a) /2x>0,h(x)在(0,+∞)递增,无最小值。
故 h(x) 的最小值Φ (a)的解析式为2a(1-ln2a) (a>o)
(Ⅲ)由(2)知Φ (a)=2a(1-ln2a)
对任意的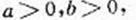
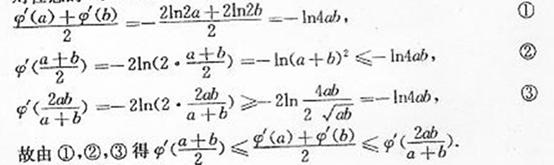
20.(本小题满分13分)
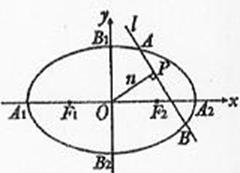 如图,椭圆C:
如图,椭圆C: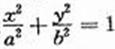 的顶点为A1,A2,B1,B2,焦点为F1,F2, | A1B1| =
的顶点为A1,A2,B1,B2,焦点为F1,F2, | A1B1| =
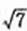 ,
,

(Ⅰ)求椭圆C的方程;
(Ⅱ)设n是过原点的直线,l是与n垂直相交于P点、与椭圆相交于A,B两点的直线,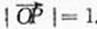 ,是否存在上述直线l使
,是否存在上述直线l使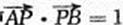 成立?若存在,求出直线l的方程;若不存在,请说明理由。
成立?若存在,求出直线l的方程;若不存在,请说明理由。
解 (Ⅰ)由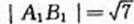 知a2+b2=7, ①
知a2+b2=7, ①
由 知a=2c,
②
知a=2c,
②
又b2=a2-c2 ③
由 ①②③解得a2=4,b2=3,
故椭圆C的方程为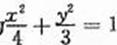 。
。
(Ⅱ)设A,B两点的坐标分别为(x1,y1)(x2,y2)
假设使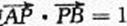 成立的直线l不存在,(Ⅰ)当l不垂直于x轴时,设l的方程为y=kx+m,
成立的直线l不存在,(Ⅰ)当l不垂直于x轴时,设l的方程为y=kx+m,
由l与n垂直相交于P点且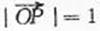 得
得
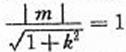 ,即m2=k2+1.
,即m2=k2+1.
∵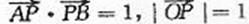 ,
,
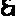
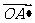
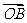 =(
=(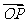 +
+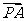 )
) (
(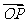 +
+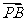 )
=
)
=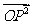 +
+ 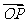

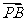 +
+ 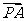

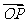 +
+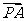

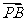 =1+0+1-1=0
=1+0+1-1=0
即X1X2+Y1Y2=0.
将y=kx+m代入椭圆方程,得
(3+4K2)X2+8kmx+ (4m2-12)=0
有求根公式可得 x1+x2=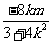 ,
x1 x2=
,
x1 x2=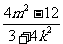 .
.
O= x1 x2 + y1y2 = x1 x2 + (kx1+m ) (kx2+m)
= x1 x2 +k2 x1 x2 +km(x1+x2)+m2
= (1+k2) x1 x2 +km (x1+x2) +m2
将 ④ 5代入上式并 化简得
(1+k2)(4m2-12)-8k2m2+m2(3+4k2)=0,
将m2=1+k2代入6并简化得-5(k2+1)=0,矛盾。
即此时直线L不存在。
()当直线L垂直于X轴 时,满足|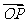 |=1的直线l的方程为x=1或x=-1.
|=1的直线l的方程为x=1或x=-1.
当x=1时,ABP的坐标分别为(1,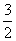 )(1.-
)(1.-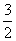 )(1.0)
)(1.0)
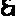
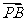 =(0,-
=(0,-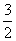 )
) 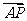 =(0,-
=(0,-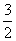 )
)
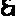
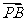
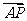 =
=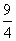
当x=-1时,同理可得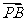
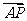
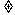 1,矛盾。即次直线来也不存在。
1,矛盾。即次直线来也不存在。
综上所述使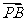
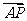 =1直线L也不存在
=1直线L也不存在
18.(本小题满分12分)
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA ⊥平面ABCD,AP=AB=2,BC=2 √ 2,E,F分别是AD,PC的重点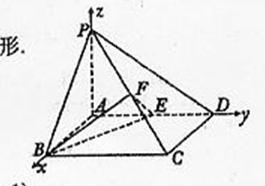
(Ⅰ)证明:PC ⊥平面BEF;
(Ⅱ)求平面BEF与平面BAP夹角的大小。
解法一 (Ⅰ)如图,以A为坐标原点,AB,AD,AP算在直线分别为x,y,z轴建立空间直角坐标系。
∵AP=AB=2,BC=AD=2√ 2,四边形ABCD是矩形。
∴A,B,C,D的坐标为A(0,0,0),B(2,0,0),C(2, 2 √ 2,0),D(0,2 √ 2,0),P(0,0,2)
又E,F分别是AD,PC的中点,
∴E(0,√ 2,0),F(1,√ 2,1)。
∴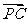 =(2,2 √ 2,-2)
=(2,2 √ 2,-2)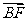 =(-1,√ 2,1)
=(-1,√ 2,1)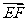 =(1,0,1),
=(1,0,1),
∴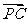 ·
·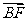 =-2+4-2=0,
=-2+4-2=0,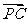 ·
·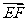 =2+0-2=0,
=2+0-2=0,
∴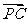 ⊥
⊥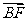 ,
,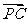 ⊥
⊥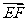 ,
,
∴PC⊥BF,PC⊥EF,BF ∩ EF=F,
∴PC⊥平面BEF
(II)由(I)知平面BEF的法向量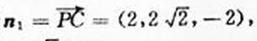
平面BAP 的法向量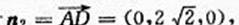
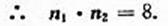 设平面BEF与平面BAP的夹角为 θ ,
设平面BEF与平面BAP的夹角为 θ ,
则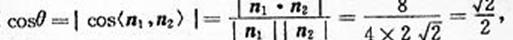
∴ θ=45℃, ∴ 平面BEF与平面BAP的夹角为45
解法二 (I)连接PE,EC在 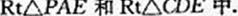
PA=AB=CD, AE=DE,
∴ PE= CE, 即 △PEC 是等腰三角形,
又F是PC 的中点,∴EF⊥PC,
又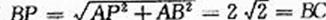 ,F是PC
的中点,
,F是PC
的中点,
∴BF⊥PC.
又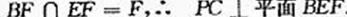

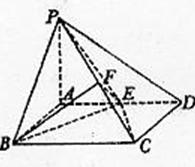
19 (本小题满分12分)
为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行出样检查,测得身高情况的统计图如下:
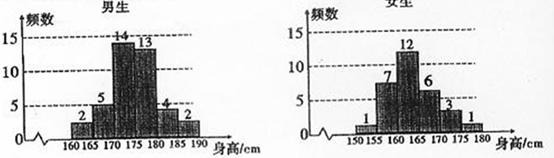
(1)估计该小男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在165~180cm之间的女生中任选2人,求至少有1人身高在170~180cm之间的概率。
解 (1)样本中男生人数为40 ,由分层出样比例为10%估计全校男生人数为400。
(2)有统计图知,样本中身高在170~185cm之间的学生有14+13+4+3+1=35人,样本容量为70 ,所以样本中学生身高在170~185cm之间的频率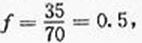 故有f估计该校学生身高在170~180cm之间的概率
故有f估计该校学生身高在170~180cm之间的概率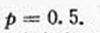
(3)样本中女生身高在165~180cm之间的人数为10,身高在170~180cm之间的人数为4。
设A表示事件“从样本中身高在165~180cm之间的女生中任选2人,求至少有1人身高在170~180cm之间”,
则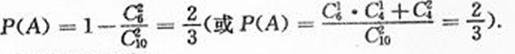
17.(本小题满分12分)
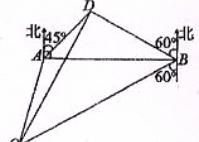
如图,A,B是海面上位于东西方向相聚5(3+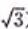 )海里的两个观测点,现位于A点北偏东45°,B点北偏西60°且与B点相距
)海里的两个观测点,现位于A点北偏东45°,B点北偏西60°且与B点相距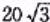 海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?
海里的C点的救援船立即前往营救,其航行速度为30海里/小时,该救援船达到D点需要多长时间?
解 由题意知AB=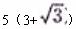 海里,
海里,
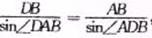 ∠ DAB=90°-60°=30°,∠ DAB=90°-45°=45°,∴∠ADB=180°-(45°+30°)=105°,在△ADB中,有正弦定理得
∠ DAB=90°-60°=30°,∠ DAB=90°-45°=45°,∴∠ADB=180°-(45°+30°)=105°,在△ADB中,有正弦定理得
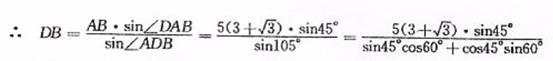
16.(本小题满分12分)
已知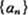 是公差不为零的等差数列,
是公差不为零的等差数列, 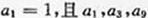 成等比数列.
成等比数列.
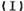 求数列
求数列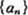 的通项;
的通项; 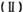 求数列
求数列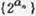 的前n项和
的前n项和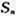
解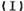 由题设知公差
由题设知公差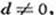
由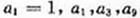 成等比数列得
成等比数列得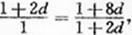
解得 (舍去)
(舍去)
故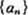 的通项
的通项
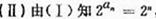 ,
,
由等比数列前n项和公式得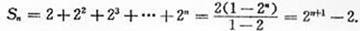
15.(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
A.(不等式选做题)不等式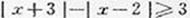 的解集为
的解集为 .
.
B.(几何证明选做题)如图,已知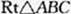 的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的图与AB交于点D,则
的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的图与AB交于点D,则 .
.
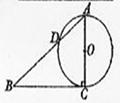
C.(坐标系与参数方程选做题)已知圆C的参数方程为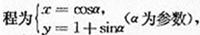 以原点为极点,x轴正半轴为极轴建立极坐标系,直线
以原点为极点,x轴正半轴为极轴建立极坐标系,直线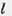 的极坐标方程为
的极坐标方程为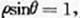 则直线
则直线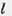 与圆C的交点的直角坐标为
与圆C的交点的直角坐标为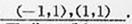
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com