
题目列表(包括答案和解析)
2.(福建卷理7)若点O和点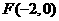 分别是双曲线
分别是双曲线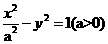 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则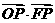 的取值范围为 ( )
的取值范围为 ( )
A. 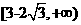 B.
B. 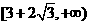 C.
C. 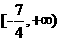 D.
D. 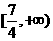
[答案]B
[解析]因为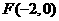 是已知双曲线的左焦点,所以
是已知双曲线的左焦点,所以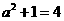 ,即
,即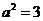 ,所以双曲线方程为
,所以双曲线方程为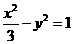 ,设点P
,设点P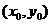 ,则有
,则有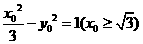 ,解得
,解得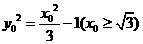 ,因为
,因为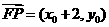 ,
,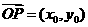 ,所以
,所以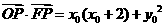 =
=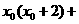
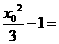
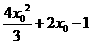 ,此二次函数对应的抛物线的对称轴为
,此二次函数对应的抛物线的对称轴为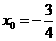 ,因为
,因为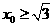 ,所以当
,所以当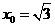 时,
时,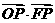 取得最小值
取得最小值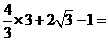
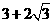 ,故
,故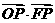 的取值范围是
的取值范围是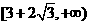 ,选B。
,选B。
[命题意图]本题考查待定系数法求双曲线方程,考查平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程序以及知识的综合应用能力、运算能力。
1.(安徽卷理5)双曲线方程为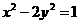 ,则它的右焦点坐标为
,则它的右焦点坐标为
A、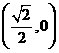 B、
B、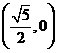 C、
C、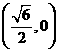 D、
D、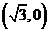
[答案]C
[解析]双曲线的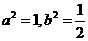 ,
,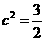 ,
,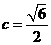 ,所以右焦点为
,所以右焦点为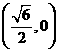 .
.
[误区警示]本题考查双曲线的交点,把双曲线方程先转化为标准方程,然后利用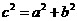 求出c即可得出交点坐标.但因方程不是标准形式,很多学生会误认为
求出c即可得出交点坐标.但因方程不是标准形式,很多学生会误认为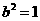 或
或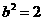 ,从而得出错误结论.
,从而得出错误结论.
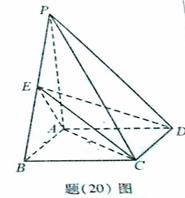
33.(重庆卷文20)如题(20)图,四棱柱P-ABCD中,底面ABCD
为矩形,PA⊥底面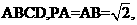 点E是棱PB的中点。
点E是棱PB的中点。
( Ⅰ)证明:AE⊥平面PBC
(Ⅱ)若AD=1,求二面角B-EC-D的平面角的余弦值。


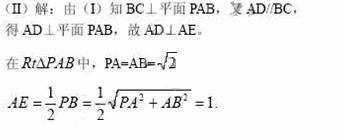
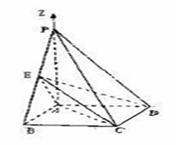

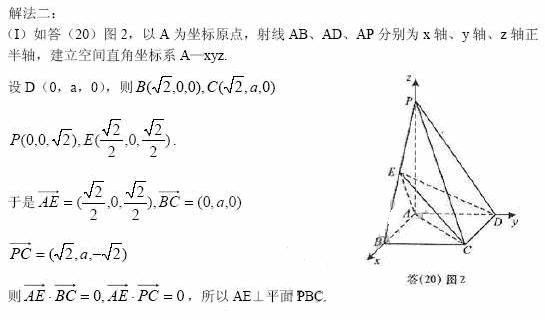

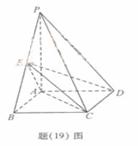
32.(重庆卷理19)如题(19)图,四棱锥P-ABCD中,底面ABCD为矩形,PA 底面ABCD,PA=AB=
底面ABCD,PA=AB=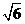 ,点E是棱PB的中点。
,点E是棱PB的中点。
(Ⅰ)求直线AD与平面PBC的距离;
(Ⅱ)若AD=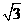 ,求二面角A-EC-D的平面角的余弦值。
,求二面角A-EC-D的平面角的余弦值。


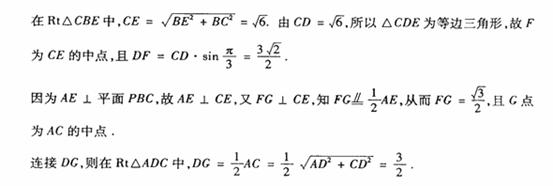
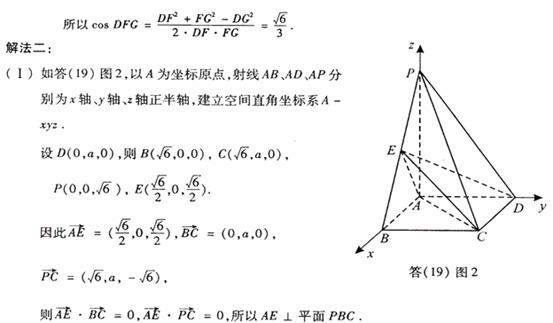


31.(浙江卷文20)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°,E为线段AB的中点,将△ADE沿直线DE翻折成△A’DE,使平面A’DE⊥平面BCD,F为线段A’C的中点。
(Ⅰ)求证:BF∥平面A’DE;
(Ⅱ)设M为线段DE的中点,求直线FM与平面A’DE所成角的余弦值。
解析:本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力。
(Ⅰ)证明:取A′D的中点G,连结GF,CE,由条件易知
FG∥CD,FG=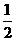 CD.
CD.
BE∥CD,BE=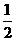 CD.
CD.
所以FG∥BE,FG=BE.
故四边形BEGF为平行四边形,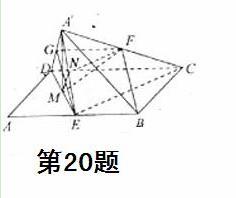 所以BF∥EG
所以BF∥EG
 因为
因为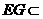 平面
平面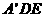 ,BF
,BF 平面
平面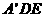
所以 BF//平面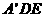
(Ⅱ)解:在平行四边形,ABCD中,设BC=a
则AB=CD=2a, AD=AE=EB=a, 连CE
因为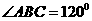
在△BCE中,可得CE=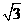 a,
a,
在△ADE中,可得DE=a,
在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE,
在正三角形A′DE中,M为DE中点,所以A′M⊥DE.
由平面A′DE⊥平面BCD,
可知A′M⊥平面BCD,A′M⊥CE.
取A′E的中点N,连线NM、NF,
所以NF⊥DE,NF⊥A′M.
因为DE交A′M于M,
所以NF⊥平面A′DE,
则∠FMN为直线FM与平面A′DE新成角.
在Rt△FMN中,NF=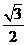 a,
MN=
a,
MN=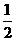 a,
FM=a
a,
FM=a
,则cos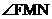 =
=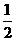 .
.
 所以直线FM与平面A′DE所成角的余弦值为
所以直线FM与平面A′DE所成角的余弦值为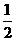 .
.
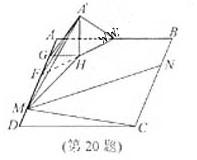
30.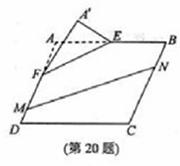 (浙江卷理20)如图,
在矩形
(浙江卷理20)如图,
在矩形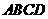 中,点
中,点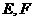 分别在线段
分别在线段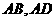 上,
上,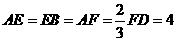 .沿直线
.沿直线 将
将
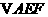 翻折成
翻折成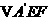 ,使平面
,使平面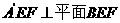 .
.
(Ⅰ)求二面角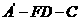 的余弦值;
的余弦值;
(Ⅱ)点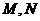 分别在线段
分别在线段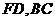 上,若沿直线
上,若沿直线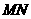 将四边形
将四边形 向上翻折,使
向上翻折,使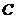 与
与 重合,求线段
重合,求线段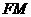 的长。
的长。
解析:本题主要考察空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同事考查空间想象能力和运算求解能力。
(Ⅰ)解:取线段EF的中点H,连结 ,因为
,因为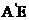 =
=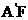 及H是EF的中点,所以
及H是EF的中点,所以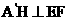 ,
,
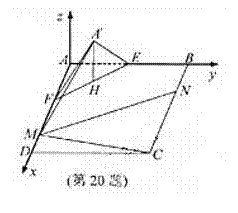 又因为平面
又因为平面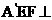 平面
平面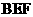 .如图建立空间直角坐标系A-xyz则
.如图建立空间直角坐标系A-xyz则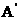 (2,2,
(2,2,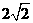 ),C(10,8,0),
),C(10,8,0),
F(4,0,0),D(10,0,0).
故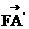 =(-2,2,2
=(-2,2,2 ),
),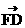 =(6,0,0).
=(6,0,0).
设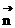 =(x,y,z)为平面
=(x,y,z)为平面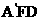 的一个法向量,
的一个法向量,
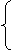 -2x+2y+2
-2x+2y+2 z=0
z=0
所以
6x=0.
取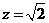 ,则
,则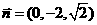 。
。
又平面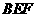 的一个法向量
的一个法向量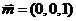 ,
,
故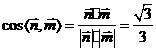 。
。
所以二面角的余弦值为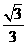
(Ⅱ)解:设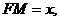 则
则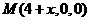 ,
,
因为翻折后,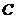 与
与 重合,所以
重合,所以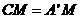 ,
,
故, 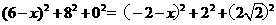 ,得
,得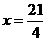 ,
,
经检验,此时点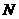 在线段
在线段 上,所以
上,所以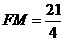 。
。
方法二:
 (Ⅰ)解:取线段
(Ⅰ)解:取线段 的中点
的中点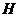 ,
,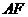 的中点
的中点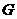 ,连结
,连结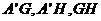 。
。
因为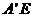 =
=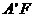 及
及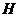 是
是 的中点,所以
的中点,所以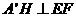
又因为平面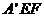
 平面
平面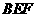 ,
,
所以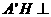 平面
平面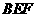 ,
,
又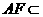 平面
平面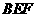 ,故
,故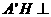
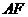 ,
,
又因为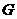 、
、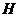 是
是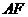 、
、 的中点,易知
的中点,易知 ∥
∥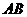 ,
,
所以

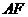 ,于是
,于是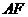
 面
面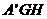 ,
,
所以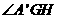 为二面角
为二面角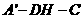 的平面角,
的平面角,
在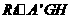 中,
中,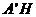 =
=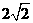 ,
, =2,
=2,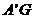 =
=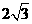
所以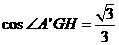 .故二面角
.故二面角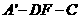 的余弦值为
的余弦值为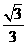 。
。
(Ⅱ)解:设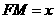 ,
,
因为翻折后,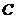 与
与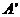 重合,所以
重合,所以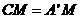 ,
,
而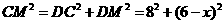 ,
,
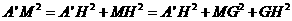
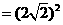
得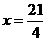 ,
,
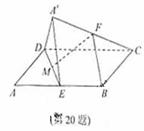 经检验,此时点
经检验,此时点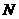 在线段
在线段 上,所以
上,所以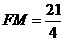 。
。
29.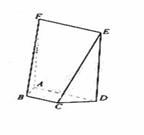 (天津卷文19)如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=
(天津卷文19)如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD=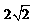 ,∠BAD=∠CDA=45°.
,∠BAD=∠CDA=45°.
(Ⅰ)求异面直线CE与AF所成角的余弦值;
(Ⅱ)证明CD⊥平面ABF;
(Ⅲ)求二面角B-EF-A的正切值。
[命题意图]本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识,考查空间想象能力,运算能力和推理论证能力.
[解析](I)解:因为四边形ADEF是正方形,所以FA//ED.故 为异面直线CE与AF所成的角.
为异面直线CE与AF所成的角.
因为FA 平面ABCD,所以FA
平面ABCD,所以FA CD.故ED
CD.故ED CD.
CD.
在Rt△CDE中,CD=1,ED=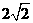 ,CE=
,CE=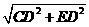 =3,故cos
=3,故cos =
=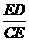 =
=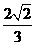 .
.
所以异面直线CE和AF所成角的余弦值为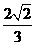 .
.
(Ⅱ)证明:过点B作BG//CD,交AD于点G,则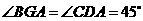 .由
.由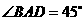 ,可得BG
,可得BG AB,从而CD
AB,从而CD AB,又CD
AB,又CD FA,FA
FA,FA AB=A,所以CD
AB=A,所以CD 平面ABF.
平面ABF.
(Ⅲ)解:由(Ⅱ)及已知,可得AG= ,即G为AD的中点.取EF的中点N,连接GN,则GN
,即G为AD的中点.取EF的中点N,连接GN,则GN EF,因为BC//AD,所以BC//EF.过点N作NM
EF,因为BC//AD,所以BC//EF.过点N作NM EF,交BC于点M,则
EF,交BC于点M,则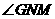 为二面角B-EF-A的平面角。
为二面角B-EF-A的平面角。
连接GM,可得AD 平面GNM,故AD
平面GNM,故AD GM.从而BC
GM.从而BC GM.由已知,可得GM=
GM.由已知,可得GM=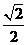 .由NG//FA,FA
.由NG//FA,FA GM,得NG
GM,得NG GM.
GM.
在Rt△NGM中,tan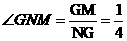 ,所以二面角B-EF-A的正切值为
,所以二面角B-EF-A的正切值为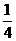 .
.
28.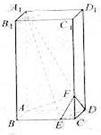 (天津卷理19)如图,在长方体
(天津卷理19)如图,在长方体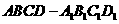 中,
中,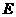 、
、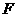 分别是棱
分别是棱 ,
,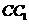 上的点,
上的点,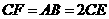 ,
,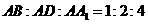
求异面直线 与
与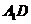 所成角的余弦值;
所成角的余弦值;
证明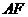
 平面
平面
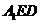
求二面角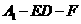 的正弦值。
的正弦值。
[命题意图]本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想象能力、运算能力和推理论证能力。
[解析]方法一:如图所示,建立空间直角坐标系,点A为坐标原点,设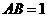 ,依题意得
,依题意得 ,
,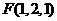 ,
,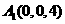 ,
,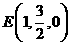
解:易得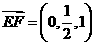 ,
,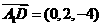
于是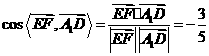
所以异面直线 与
与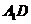 所成角的余弦值为
所成角的余弦值为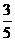
证明:已知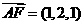 ,
,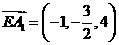 ,
,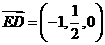
于是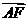 ·
·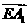 =0,
=0,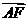 ·
·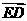 =0.因此,
=0.因此,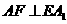 ,
,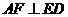 ,又
,又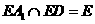
所以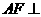 平面
平面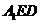
(3)解:设平面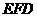 的法向量
的法向量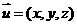 ,则
,则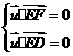 ,即
,即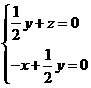
不妨令X=1,可得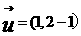 。由(2)可知,
。由(2)可知,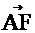 为平面
为平面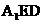 的一个法向量。
的一个法向量。
于是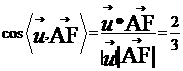 ,从而
,从而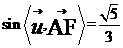
所以二面角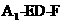 的正弦值为
的正弦值为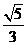
方法二:(1)解:设AB=1,可得AD=2,AA1=4,CF=1.CE=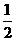
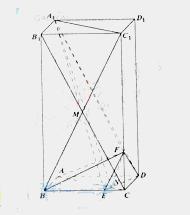 链接B1C,BC1,设B1C与BC1交于点M,易知A1D∥B1C,由
链接B1C,BC1,设B1C与BC1交于点M,易知A1D∥B1C,由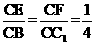 ,可知EF∥BC1.故
,可知EF∥BC1.故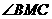 是异面直线EF与A1D所成的角,易知BM=CM=
是异面直线EF与A1D所成的角,易知BM=CM=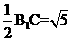 ,所以
,所以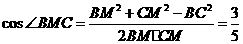 ,所以异面直线FE与A1D所成角的余弦值为
,所以异面直线FE与A1D所成角的余弦值为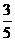
(2)证明:连接AC,设AC与DE交点N 因为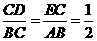 ,所以
,所以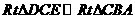 ,从而
,从而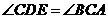 ,又由于
,又由于 ,所以
,所以 ,故AC⊥DE,又因为CC1⊥DE且
,故AC⊥DE,又因为CC1⊥DE且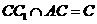 ,所以DE⊥平面ACF,从而AF⊥DE.
,所以DE⊥平面ACF,从而AF⊥DE.
连接BF,同理可证B1C⊥平面ABF,从而AF⊥B1C,所以AF⊥A1D因为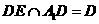 ,所以AF⊥平面A1ED
,所以AF⊥平面A1ED
(3)解:连接A1N.FN,由(2)可知DE⊥平面ACF,又NF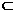 平面ACF, A1N
平面ACF, A1N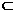 平面ACF,所以DE⊥NF,DE⊥A1N,故
平面ACF,所以DE⊥NF,DE⊥A1N,故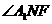 为二面角A1-ED-F的平面角
为二面角A1-ED-F的平面角
易知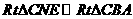 ,所以
,所以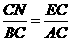 ,又
,又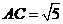 所以
所以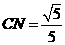 ,在
,在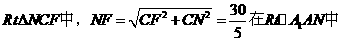
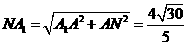
连接A1C1,A1F 在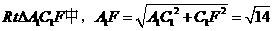
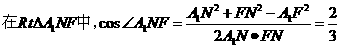 。所以
。所以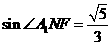
所以二面角A1-DE-F正弦值为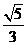 。
。
27.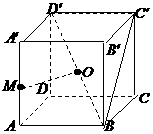
 (四川卷文18)在正方体ABCD-A′B′C′D′中,点M
(四川卷文18)在正方体ABCD-A′B′C′D′中,点M
是棱AA′的中点,点O是对角线BD′的中点.
 (Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅰ)求证:OM为异面直线AA′和BD′的公垂线;
(Ⅱ)求二面角M-BC′-B′的大小;



26.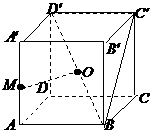 (四川卷理18)已知正方体
(四川卷理18)已知正方体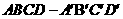 的棱长为1,点
的棱长为1,点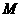 是棱
是棱 的中点,点
的中点,点 是对角线
是对角线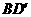 的中点.
的中点.
(Ⅰ)求证: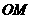 为异面直线
为异面直线 和
和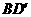 的公垂线;
的公垂线;
(Ⅱ)求二面角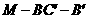 的大小;
的大小;
(Ⅲ)求三棱锥 的体积.
的体积.



湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com