
题目列表(包括答案和解析)
(13)某高校甲、乙、丙、丁四个专业分别有150、150、400、300名学生,为了解学生的就业倾向,用分层抽样的方法从该校这四个专业共抽取40名学生进行调查,应在丙专业抽取的学生人数为 .
(14)执行右图所示的程序框图,输入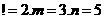 ,则输出的
,则输出的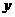 的值是
.
的值是
.
(15)已知双曲线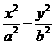 =1(
=1(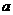 >0,
>0, 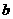 >0)和椭圆
>0)和椭圆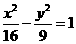 有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为
.
有相同的焦点,且双曲线的离心率是椭圆离心率的两倍,则双曲线的方程为
.
(16)已知函数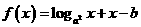 (
(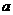 >0,且
>0,且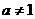 ).
).
当2<a<3<b<4时,函数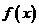 的零点
的零点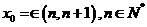 ,则
,则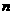 =
.
=
.
①
设集合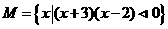 ,
,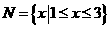 ,则
,则
(A)
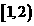 (B)
(B)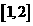 (C)
(C)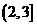 (D)
(D)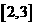
(2)复数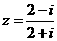 (
(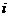 虚数单位)在复平面内对应的点所在象限为
虚数单位)在复平面内对应的点所在象限为
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
(3)若点(a,9)在函数y=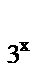 的图像上,则tan
的图像上,则tan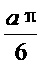 的值为 ( )
的值为 ( )
(A)0
(B)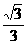 (C)1
(D)
(C)1
(D)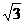
(4)曲线y=x3+11在点P(1,12)处的切线与y轴交点的纵坐标是
(A)-9 (B)-3 (C)9 (D)15
(5) a,b,c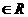 ,命题“a+b+c=3,则a2+b2+c2 ≥ 3”的否命题是
,命题“a+b+c=3,则a2+b2+c2 ≥ 3”的否命题是
(A)若a+b+c ≠3,则a2+b2+c2<3 (B)若 a+b+c=3,则a2+b2+c2<3
(C) 若a+b+c≠3,则a2+b2+c2 ≥ 3 (D) 若a+b+c ≥ 3,则a2+b2+c2=3
(6)若函数f(x)=sin x(
x( >0)在区间[0,
>0)在区间[0, 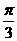 ]上单调递增,在区间[
]上单调递增,在区间[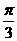 ,
,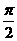 ]上单调递减,则
]上单调递减,则 =
=
(A)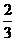 (B)
(B) 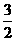 (C) 2 (D)3
(C) 2 (D)3
(7)设变量x,y满足约束条件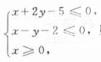 ,则目标函数z=2x+3y+1的最大值为
,则目标函数z=2x+3y+1的最大值为
(A)11 (B)10 (C)9 (D)8.5
(8)某产品的广告费用x与销售额y的统计数据如下表:

根据上表可得回归方程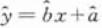 中的
中的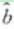 为9.4,据此模型预报广告费用为6万元时销售额为
为9.4,据此模型预报广告费用为6万元时销售额为
(A)63.6 万元 (B)65.6万元 (C)67.7万元 (D)72.0万元
(9)设M(x0,y0)为抛物线C:x2=8y上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则 y的取值范围是
(A)(0,1) (B) [0,2 ] (C)( 2,+∞) (D)[2,+ ∞)
(10)函数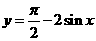 的图像大致是
的图像大致是
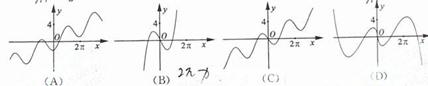
(11)右图是长和宽分别相等的两个矩形,结合下列三个命题:①存在三棱柱,其正(主)视图、俯视图如右图;②存在四棱柱,其正(主)视图、俯视图如右图;③存在圆柱,其正(主)视图、俯视图如右图。其中真命题的个数是
 (A)3
(B)2
(A)3
(B)2
(C)1 (D)0
(12)设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若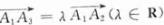 ,
,
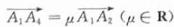 ,且
,且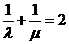 ,则称A3A4调和分割A1,A2.已知C(c,0),D(d,0)((c,d,∈ R)调和分割点A(1,0),B(,1,0) ,则下面说法正确的是
,则称A3A4调和分割A1,A2.已知C(c,0),D(d,0)((c,d,∈ R)调和分割点A(1,0),B(,1,0) ,则下面说法正确的是
(A)C可能是限度那AB的中点
(B)D可能是限度那AB的中点
(C)C,D可能同时在线段AB上
(D)C,D不可能同时在线段AB的延长线上
第 Ⅱ卷(共90分)
21.(本小题满分14分)
在平面直角坐标系xOy,直线l:x=-2交x轴于点A,设P是l上一点,M是线段OP的垂直平分线上一点,且满足∠MPO.
(1)当点P在l上运动时,求点M的轴上E的方程;
(2)已知T(1,-1),设H是E上动点,求 +
+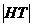 的最小值,并给出此时点H的坐标。;
的最小值,并给出此时点H的坐标。;
(3)过点T(1,-1)且不平行于y轴的直线l1与轨迹E有且只有两个不同的交点,求直线l1的斜率k的取值范围。
20.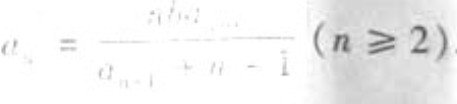 (本小题满分14分)
(本小题满分14分)
设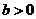 ,数列
,数列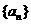 满足
满足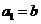 ,
,
(1)求数列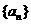 的通项公式;
的通项公式;
(2)证明:对于一切正整数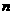 ,
,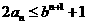
19.(本小题满分14分)
设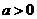 ,讨论函数
,讨论函数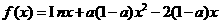 的单调性。
的单调性。
18.(本小题满分13分)
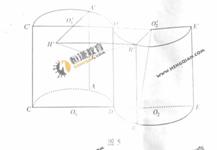
如图所示的几何体是将高为2,底面半径为1的直圆柱沿过轴的平面切开后,将其中沿切面向右水平平移后得到的A,A′、B,B′分别为 ,的中点,O1O2O′1O′2分别为CD,
,的中点,O1O2O′1O′2分别为CD,
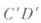 ,DE,
,DE, 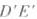 的中点.
的中点.
(1)证明: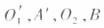 四点共面;
四点共面;
(2)设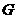 为
为 中点,延长
中点,延长 到
到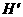 ,使得到的
,使得到的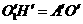 ,证明:
,证明: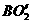 ⊥平面
⊥平面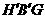
(16)(本小题满分12分)
已知函数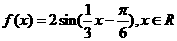 。
。
(1)
求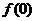 的值;
的值;
(2)
设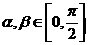 ,
,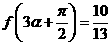 ,
,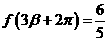 ,求
,求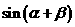 的值。
的值。
17.(本小题满分13分)
在某次测验中,有6位同学的平均成均为75分,用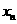 表示编号为n(n=1,2, …,6)的同学所得成绩,且前5位同学的成绩如下:
表示编号为n(n=1,2, …,6)的同学所得成绩,且前5位同学的成绩如下:

(1)
求第6位同学的成绩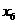 ,及这6位同学成绩的标准差s;
,及这6位同学成绩的标准差s;
(2) 从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率。
(二)选做题(14-15小题,考生只能从中选做一题)
14. (坐标系与参数方程选做题)已知两曲线参数方程分别为
(坐标系与参数方程选做题)已知两曲线参数方程分别为
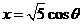
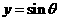 (
(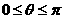 )和
)和
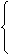
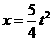
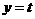 (
(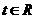 ),它们的交点坐标为
),它们的交点坐标为
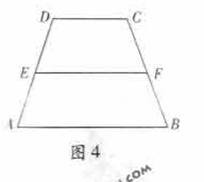
15.(几何证明选讲选做题)如图4,在梯形ABCD中,AB∥CD,AB=4,CD=2.E,F分别为AD,BC上点,且EF=3.EF∥AB,则梯形ABFE与梯形EFCD的面积比为
11.已知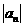 是递增等比数列,
是递增等比数列,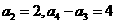 ,则此数列的公比
,则此数列的公比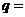
12.设函数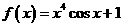 。若
。若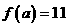 ,则
,则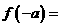
13.为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间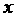 (单位:小时)与当天投篮命中率
(单位:小时)与当天投篮命中率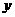 之间的关系:
之间的关系:
时间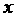 |
1 |
2 |
3 |
4 |
5 |
命中率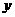 |
0.4 |
0.5 |
0.6 |
0.6 |
0.4 |
小李这5天的平均投篮命中率为 ;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 .
10.设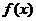 ,
,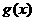 ,
,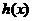 是R上的任意实值函数,如下定义两个函数
是R上的任意实值函数,如下定义两个函数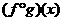 和
和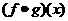 ;对任意
;对任意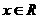 ,
,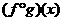 =
=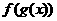 ;
;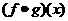 =
=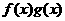 ,则下列等式恒成立的是
,则下列等式恒成立的是
A. 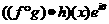 =
=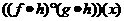
B. 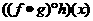 =
=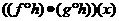
C. 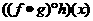 =
=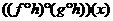
D. 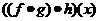 =
=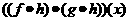
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com