
题目列表(包括答案和解析)
4.已知集合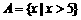 ,集合
,集合 ,若命题“
,若命题“ ”是命 题“
”是命 题“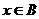 ”的充分不必要条件,则实数
”的充分不必要条件,则实数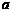 的取值范围是 ;
的取值范围是 ;
3. 已知等比数列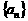 中,各项都是正数,且
中,各项都是正数,且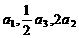 成等差数列,
成等差数列,
则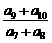 =
;
=
;
2.抛物线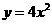 的焦点到准线的距离是 ;
的焦点到准线的距离是 ;
1.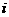 是虚数单位,复数
是虚数单位,复数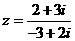 的虚部是 ;
的虚部是 ;
20.(16分)已知函数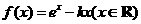 。
。
(1)若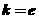 ,试确定函数
,试确定函数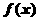 的单调区间;
的单调区间;
(2)若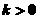 且对任意
且对任意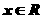 ,
,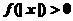 恒成立,试确定实数
恒成立,试确定实数 的取值范围;
的取值范围;
(3)设函数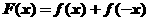 ,求证:
,求证: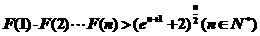
19、(本题满分16分)第(1)小题满分6分,第(2)小题满分6分,第(3)小题满分6分。
设等比数列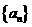 的首项为
的首项为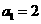 ,公比为
,公比为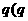 为正整数),且满足
为正整数),且满足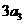 是
是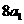 与
与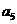 的等差中项;数列
的等差中项;数列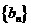 满足
满足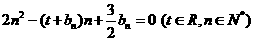 。
。
(1) 求数列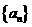 的通项公式;
的通项公式;
(2) 试确定实数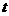 的值,使得数列
的值,使得数列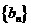 为等差数列;
为等差数列;
(3) 当数列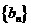 为等差数列时,对每个正整数
为等差数列时,对每个正整数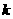 ,在
,在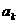 和
和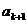 之间插入
之间插入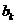 个2,得到一个新数列
个2,得到一个新数列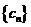 。设
。设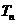 是数列
是数列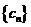 的前
的前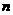 项和,试求满足
项和,试求满足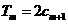 的所有正整数
的所有正整数 。
。
18、(本题满分15分)已知圆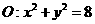 交
交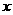 轴于
轴于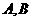 两点,曲线
两点,曲线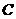 是以
是以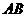 为长轴,直线
为长轴,直线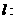
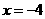 为准线的椭圆.
为准线的椭圆.
(1)求椭圆的标准方程;
 (2)若
(2)若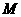 是直线
是直线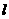 上的任意一点,以
上的任意一点,以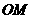 为直径的圆
为直径的圆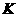 与圆
与圆 相交于
相交于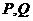 两点,求证:直线
两点,求证:直线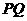 必过定点
必过定点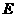 ,并求出点
,并求出点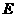 的坐标。
的坐标。
17、(本题满分15分)第(1)小题满分7分,第(2)小题满分8分。
如图1, ,
,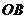 是某地一个湖泊的两条互相垂直的湖堤,线段
是某地一个湖泊的两条互相垂直的湖堤,线段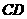 和曲线段
和曲线段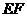 分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥
分别是湖泊中的一座栈桥和一条防波堤。为观光旅游的需要,拟过栈桥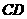 上某点
上某点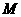 分别修建与
分别修建与 ,
,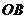 平行的栈桥
平行的栈桥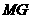 、
、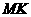 ,且以
,且以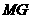 、
、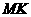 为边建一个跨越水面的三角形观光平台
为边建一个跨越水面的三角形观光平台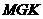 。建立如图2所示的直角坐标系,测得线段
。建立如图2所示的直角坐标系,测得线段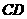 的方程是
的方程是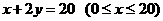 ,曲线段
,曲线段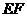 的方程是
的方程是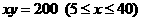 ,设点
,设点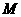 的坐标为
的坐标为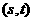 ,记
,记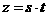 。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
。(题中所涉及的长度单位均为米,栈桥和防波堤都不计宽度)
(1)求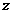 的取值范围;
的取值范围;
(2)试写出三角形观光平台 面积
面积 关于
关于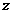 的函数解析式,并求出该面积的最小值。
的函数解析式,并求出该面积的最小值。
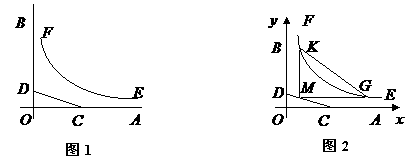
15(本题满分14分)
在△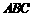 中,已知
中,已知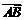 ·
· =9,sin
=9,sin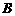 =cos
=cos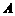 sin
sin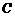 ,面积S
,面积S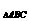 =6.
=6.
(Ⅰ)求△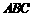 的三边的长;
的三边的长;
(Ⅱ)设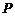 是△
是△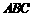 (含边界)内一点,
(含边界)内一点,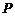 到三边
到三边 ,
,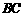 ,
,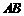 的距离分别为x,y和z,求x+y+z的取值范围.
的距离分别为x,y和z,求x+y+z的取值范围.
16.(本题满分14分)如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°。
(Ⅰ)证明:BD⊥AA1;(Ⅱ)
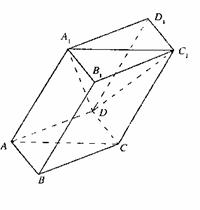 在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由。
在直线CC1上是否存在点P,使BP//平面DA1C1?若存在,求出点P的位置;若不存在,说明理由。
14、设函数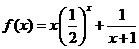 ,
, 为坐标原点,
为坐标原点,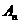 为函数
为函数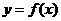 图象上横坐标为
图象上横坐标为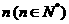 的点,向量
的点,向量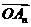 与向量
与向量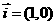 的夹角为
的夹角为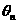 ,则满足
,则满足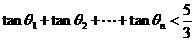 的最大整数
的最大整数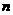 的值为
。
的值为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com