
题目列表(包括答案和解析)
21.(本小题满分14分)
已知直线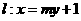 过椭圆
过椭圆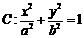 的右焦点F,抛物线:
的右焦点F,抛物线: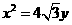 的焦点为椭圆
的焦点为椭圆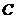 的上顶点,且直线
的上顶点,且直线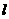 交椭圆
交椭圆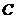 于
于 、
、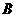 两点,点
两点,点 、F、
、F、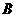 在直线
在直线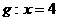 上的射影依次为点
上的射影依次为点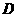 、
、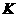 、
、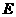 .
.
(1)求椭圆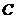 的方程;
的方程;
(2)若直线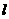 交y轴于点
交y轴于点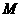 ,且
,且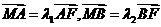 ,当
,当 变化时,探求
变化时,探求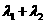
的值是否为定值?若是,求出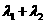 的值,否则,说明理由;
的值,否则,说明理由;
(3)连接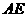 、
、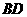 ,试探索当
,试探索当 变化时,直线
变化时,直线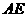 与
与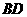 是否相交于定点?
是否相交于定点?
若是,请求出定点的坐标,并给予证明;否则,说明理由.
20.(本小题满分13分)
已知函数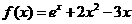 .
.
(1)求证函数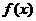 在区间
在区间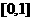 上存在唯一的极值点,并用二分法求函数取得极值时相应
上存在唯一的极值点,并用二分法求函数取得极值时相应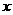 的近似值(误差不超过
的近似值(误差不超过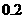 );(参考数据
);(参考数据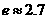 ,
,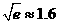 ,
,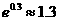 )
)
(2)当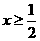 时,若关于
时,若关于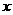 的不等式
的不等式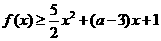 恒成立,试求实数
恒成立,试求实数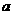 的取值范围.
的取值范围.
19. (本小题满分12分)
已知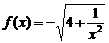 ,数列
,数列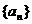 的前n项和为
的前n项和为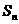 ,点
,点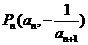 在曲线
在曲线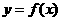 上
上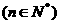 ,且
,且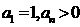 。
。
(1)求数列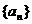 的通项公式;
的通项公式;
(2)数列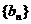 的前n项和为
的前n项和为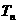 ,且满足
,且满足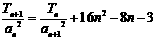 ,
,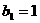 ,
,
求证:数列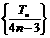 是等差数列,并求数列
是等差数列,并求数列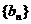 的通项公式;
的通项公式;
18.
 (本题满分12分)
(本题满分12分)
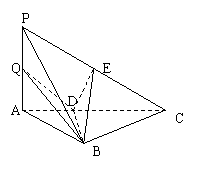
如图,三棱锥P-ABC中,PA⊥底面ABC,AB⊥BC,DE垂直平分线段PC,
且分别交AC、PC于D、E两点,又PB=BC,PA=AB。
(1)求证:PC⊥平面BDE;
(2)若点Q是线段PA上任一点,判断BD、DQ的位置关系,
并证明你的结论;
(3)若AB=2,求三棱锥B-CED的体积
17. (本小题满分12分)
为了迎接省运会,为了降低能源损耗,鹰潭市体育馆的外墙需要建造隔热层.体育馆要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用C(单位:万元)与隔热层厚度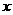 (单位:cm)满足关系:
(单位:cm)满足关系: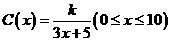 ,若不建隔热层,每年能源消耗费用为8万元.设
,若不建隔热层,每年能源消耗费用为8万元.设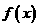 为隔热层建造费用与20年的能源消耗费用之和.
为隔热层建造费用与20年的能源消耗费用之和.
(1)求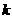 的值及
的值及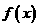 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用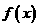 达到最小,并求最小值
达到最小,并求最小值
16.(本小题满分12分)
在△ABC中,内角A,B,C所对边长分别为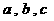 ,
,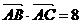 ,
,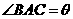 ,
,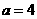 .
.
(1)求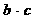 的最大值及
的最大值及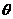 的取值范围;
的取值范围;
(2)求函数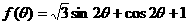 的最大值和最小值.
的最大值和最小值.
15. 设函数f(x)=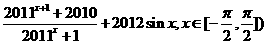 的最大值为
的最大值为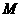 ,最小值为
,最小值为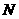 ,
,
那么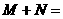 .
.
14. 直线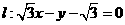 与抛物线
与抛物线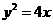 相交于A、B两点,与x轴相交于点F,若
相交于A、B两点,与x轴相交于点F,若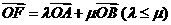 ,则
,则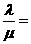 .
.
13. 若不等式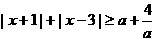 对任意的实数
对任意的实数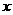 恒成立,则实数
恒成立,则实数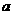 的取值范围是 .
的取值范围是 .
12. 程序框图如下:
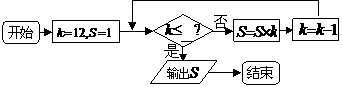
如果上述程序运行的结果为S=132,那么判断框中横线上应填入的数字是________ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com