
题目列表(包括答案和解析)
(1)已知集合A={x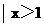 },B={x
},B={x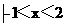 }},则A
}},则A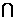 B=
B=
(A) {x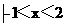 }} (B){x
}} (B){x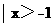 } (C){x
} (C){x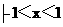 }} (D){x
}} (D){x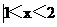 }}
}}
(2)i为虚数单位,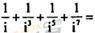
(A)0 (B)2i (C)-2i (D)4i
(3)已知向量a=(2,1),b=(-1,k),a·(2a-b)=0,则k
(A)-12 (B)-6 (C)6 (D)12
(4)已知命题P: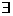 n∈N,2n>1000,则
n∈N,2n>1000,则 p为
p为
(A)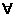 n∈N,2n≤1000 (B)
n∈N,2n≤1000 (B)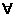 n∈N,2n>1000
n∈N,2n>1000
(C)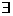 n∈N,2n≤1000
(D)
n∈N,2n≤1000
(D)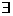 n∈N,2n<1000
n∈N,2n<1000
(5)若等比数列{an}满足anan+1=16n,则公比为
(A)2 (B)4 (C)8 (D)16
(6)若函数f(x)=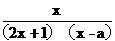 为奇函数,则a=
为奇函数,则a=
(A)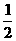 (B)
(B)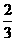 (C)
(C)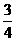 (D)1
(D)1
(7)已知F是抛物线y2=x的焦点,A,B是该抛物线上的两点,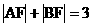 ,则线段AB的中点到y轴的距离为
,则线段AB的中点到y轴的距离为
(A)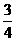 (B)1
(C)
(B)1
(C)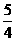 (D)
(D)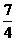
(8)一个正三棱柱的侧棱长和底面边长相等,体积为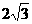 ,它的三视图中的俯视图如右图所示,
,它的三视图中的俯视图如右图所示,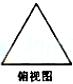 左视图是一个矩形,则这个矩形的面积是
左视图是一个矩形,则这个矩形的面积是
(A)4
(B)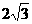 (C)2
(D)
(C)2
(D)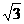
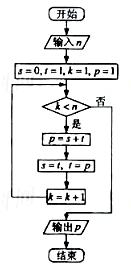
(9)执行右面的程序框图,如果输入的n是4,则输出的P是
(A) 8
(B) 5
(C) 3
(D) 2
(10)已知球的直径SC=4,。A.,B是该球球面上的两点,AB=2,∠ASC=∠BSC=45°,则棱锥S-ABC的体积为
(A)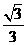 (B)
(B)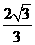
(C) 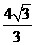 (D)
(D)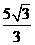
(11)函数f(x)的定义域为R,f(-1)=2,对任意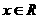 ,f(x)>2,则f(x)>2x+4的解集为
,f(x)>2,则f(x)>2x+4的解集为
(A)(-1,1)
(B)(-1,+ (C)(-
(C)(- ,-1)
(D)(-
,-1)
(D)(- ,+
,+ )
)
(12)已知函数f(x)=Atan(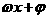 )
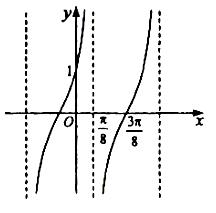
)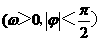 ,Y=f(x)的部分图像如图,则
,Y=f(x)的部分图像如图,则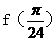 =
=
(A)2+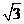 (B)
(B)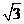
(C) 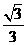 (D)
(D)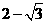
第Ⅱ卷
本卷包括必考题和选考题两部分。第13题~第21题为必考题,每个试题考生都必须作答。第22题~第24题为选考题,考生根据要求作答。
21. 本题设有(1)、(2)、(3)三个选考题,每题7分,请考生任选2题做答,满分14分,如果多做,则按所做的前两题计分,做答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中。
(1)(本小题满分7分)选修4-2:矩阵与变换
设矩阵 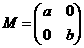 (其中a>0,b>0).
(其中a>0,b>0).
(I)若a=2,b=3,求矩阵M的逆矩阵M-1;
(II)若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C’: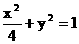 ,求a,b的值.
,求a,b的值.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在直接坐标系 中,直线l的方程为x-y+4=0,曲线C的参数方程为
中,直线l的方程为x-y+4=0,曲线C的参数方程为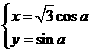 .
.
(I)已知在极坐标(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为(4,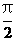 ),判断点P与直线l的位置关系;
),判断点P与直线l的位置关系;
(II)设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
(3)(本小题满分7分)选修4-5:不等式选讲
设不等式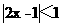 的解集为M.
的解集为M.
(I)求集合M;
(II)若a,b∈M,试比较ab+1与a+b的大小.
20.(本小题满分14分)
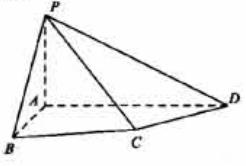 如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD中,AB⊥AD,AB+AD=4,CD=
如图,四棱锥P-ABCD中,PA⊥底面ABCD,四边形ABCD中,AB⊥AD,AB+AD=4,CD=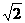 ,
,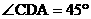 .
.
(I)求证:平面PAB⊥平面PAD;
(II)设AB=AP.
(i)若直线PB与平面PCD所成的角为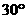 ,求线段AB的长;
,求线段AB的长;
(ii)在线段AD上是否存在一个点G,使得点G到点P,B,C,D的距离都相等?说明理由。
19.(本小题满分13分)
某产品按行业生产标准分成8个等级,等级系数X依次为1,2,……,8,其中X≥5为标准A,X≥3为标准B,已知甲厂执行标准A生产该产品,产品的零售价为6元/件;乙厂执行标准B生产该产品,产品的零售价为4元/件,假定甲、乙两厂得产品都符合相应的执行标准
(I)已知甲厂产品的等级系数X1的概率分布列如下所示:

且X1的数字期望EX1=6,求a,b的值;
(II)为分析乙厂产品的等级系数X2,从该厂生产的产品中随机抽取30件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
用这个样本的频率分布估计总体分布,将频率视为概率,求等级系数X2的数学期望.
 在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
在(I)、(II)的条件下,若以“性价比”为判断标准,则哪个工厂的产品更具可购买性?说明理由.
注:(1)产品的“性价比”= ;
;
(2)“性价比”大的产品更具可购买性.
18.(本小题满分13分)
某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式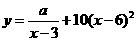 ,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克。
(I)求a的值
(II)若该商品的成品为3元/千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大。
17.(本小题满分13分)
已知直线l:y=x+m,m∈R。
(I)若以点M(2,0)为圆心的圆与直线l相切与点P,且点P在y轴上,求该圆的方程;
(II)若直线l关于x轴对称的直线为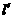 ,问直线
,问直线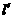 与抛物线C:x2=4y是否相切?说明理由。
与抛物线C:x2=4y是否相切?说明理由。
16.(本小题满分13分)
已知等比数列{an}的公比q=3,前3项和S3=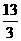 。
。
(I)求数列{an}的通项公式;
(II)若函数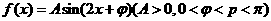 在
在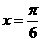 处取得最大值,且最大值为a3,求函数f(x)的解析式。
处取得最大值,且最大值为a3,求函数f(x)的解析式。
15.设V是全体平面向量构成的集合,若映射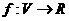 满足:对任意向量
满足:对任意向量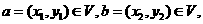 以及任意
以及任意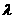 ∈R,均有
∈R,均有
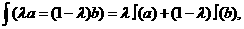
则称映射f具有性质P。
先给出如下映射:
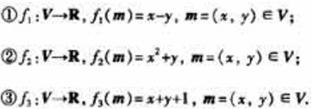

其中,具有性质P的映射的序号为________。(写出所有具有性质P的映射的序号)
14.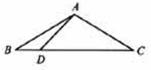 如图,△ABC中,AB=AC=2,BC=
如图,△ABC中,AB=AC=2,BC=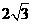 ,点D 在BC边上,∠ADC=45°,则AD的长度等于______。
,点D 在BC边上,∠ADC=45°,则AD的长度等于______。
13.何种装有形状、大小完全相同的5个球,其中红色球3个,黄色球2个。若从中随机取出2个球,则所取出的2个球颜色不同的概率等于_______。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com