
题目列表(包括答案和解析)
(1)
已知全集U=R,集合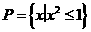 ,那么
,那么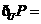
(A)(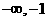 ) (B)(
) (B)(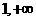 ) (C)(-1,1) (D)
) (C)(-1,1) (D)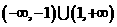
(2)复数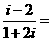
(A)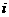 (B )
(B )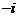 (C)
(C)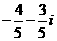 (D)
(D)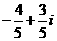
(3)如果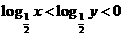 ,那么
,那么
(A)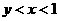 (B)
(B)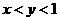 (C)
(C)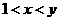 (D)
(D)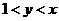
(4)若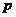 是真命题,
是真命题,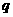 是假命题,则
是假命题,则
(A)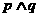 是真命题 (B)
是真命题 (B)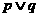 是假命题
是假命题
 (C)
(C)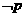 是真命题
(D)
是真命题
(D)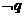 是真命题
是真命题
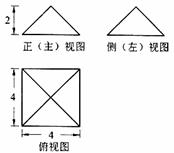
(5)某四棱锥的三视图如图所示,该四棱锥的表面积是
(A)32
(B)16+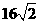
(C)48
(D)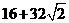
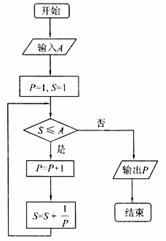
(6)执行如图所示的程序框图,若输入A的值为2,则输出的P值为
(A)2
(B)3
(C)4
(D)5
(7)某车间分批生产某种产品,每批的生产准备费用为800元。若每批生产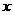 件,则平均仓储时间为
件,则平均仓储时间为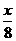 天,且每件产品每天的仓储费用为1元。为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品
天,且每件产品每天的仓储费用为1元。为使平均到每件产品的生产准备费用与仓储费用之和最小,每批应生产产品
(A)60件 (B)80件 (C)100件 (D)120件
(8)已知点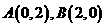 。若点
。若点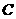 在函数
在函数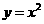 的图象上,则使得
的图象上,则使得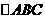 的面积为2的点
的面积为2的点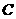 的个数为
的个数为
(A)4 (B)3 (C)2 (D)1
22.(本小题满分14分)
已知a,b为常数,且a≠0,函数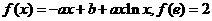 (e=2.71828…是自然对数的底数).
(e=2.71828…是自然对数的底数).
(I) 求实数b的值;
(II)求函数f(x)的单调区间;
(III)当a=1时,是否同时存在实数m和M(m<M),使得对每一个t∈[m,M],直线y=t与曲线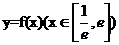 都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
都有公共点?若存在,求出最小的实数m和最大的实数M;若不存在,说明理由.
21.(本小题满分12分)
设函数f(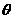 )=
)=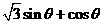 ,其中,角
,其中,角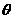 的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且
的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且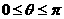 .
.
(1)若点P的坐标为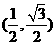 ,求
,求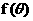 的值;
的值;
(II)若点P(x,y)为平面区域Ω: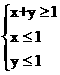 ,上的一个动点,试确定角
,上的一个动点,试确定角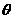 的取值范围,并求函数
的取值范围,并求函数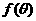 的最小值和最大值.
的最小值和最大值.
20.(本小题满分12分)
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,点E在线段AD上,且CE∥AB。
(1) 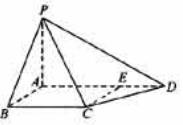 求证:CE⊥平面PAD;
求证:CE⊥平面PAD;
(11)若PA=AB=1,AD=3,CD=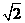 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积
19.(本小题满分12分)
某日用品按行业质量标准分成五个等级,等级系数X依次为1,2,3,4,5.现从一批该日用品中随机抽取20件,对其等级系数进行统计分析,得到频率分布表如下:
|
x |
1 |
2 |
3 |
4 |
5 |
|
f |
a |
0.2 |
0.45 |
b |
c |
(1) 若所抽取的20件日用品中,等级系数为4的恰有3件,等级系数为5的恰有2件,求a、b、c的值;
(11) 在(1)的条件下,将等级系数为4的3件日用品记为x1, x2, x3,等级系数为5的2件日用品记为y1,y2,现从x1, x2, x3, y1, y2,这5件日用品中任取两件(假定每件日用品被取出的可能性相同),写出所有可能的结果,并求这两件日用品的等级系数恰好相等的概率.
18.(本小题满分12分)
如图,直线l :y=x+b与抛物线C :x2=4y相切于点A。
(1) 求实数b的值;
(11) 求以点A为圆心,且与抛物线C的准线相切的圆的方程.
17.(本小题满分12分)
已知等差数列{an}中,a1=1,a3=-3.
(I)求数列{an}的通项公式;
(II)若数列{an}的前k项和Sk=-35,求k的值.
16.商家通常依据“乐观系数准则”确定商品销售价格,即根据商品的最低销售限价a,最高销售限价b(b>a)以及常数x(0<x<1)确定实际销售价格c=a+x(b-a),这里,x被称为乐观系数.
经验表明,最佳乐观系数x恰好使得(c-a)是(b-c)和(b-a)的等比中项,据此可得,最佳乐观系数x的值等于_____________.
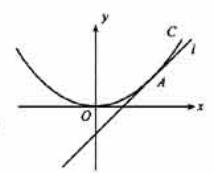
15.如图,正方体ABCD-A1B1C1D1中,AB=2。,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于_____________.
14.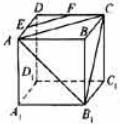 若△ABC的面积为
若△ABC的面积为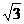 ,BC=2,C=
,BC=2,C= ,则边AB的长度等于_____________.
,则边AB的长度等于_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com