
题目列表(包括答案和解析)
18.不论m为何实数,方程 (3m+4)x+(5-2m)y+7m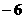 =0 所表示的直线总过一定点,则该点的坐标为
.
=0 所表示的直线总过一定点,则该点的坐标为
.
17.已知5<x<7, 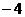 <y<3, 则x
<y<3, 则x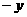 的取值范围是
.
的取值范围是
.
16.由两点A(1, 2), B(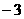 , 4) 所确定的直线的斜率为
.
, 4) 所确定的直线的斜率为
.
1、设全集为S, 对任意子集合A, B若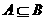 , 则下列集合为空集的是( )
, 则下列集合为空集的是( )
(A)
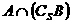 (B)
(B) 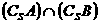 (C)
(C) 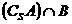 (D)
(D) 
2
不等式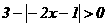 的解集是( )
的解集是( )
(A)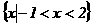 (B)
(B)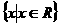 (C)
(C)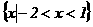
(D){x|x<-2或x>1}
3
不等式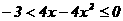 的解集是( )
的解集是( )
(A){x|x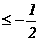 或x
或x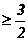 } (B){x|
} (B){x|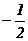 <x<
<x<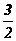 }
}
(C){x|x≤0或x≥1} (D){x|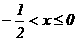 或
或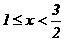 }
}
4
“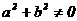 ”的含义是( )
”的含义是( )
(A)a, b全不为0 (B) a, b不全为0 (C) a, b至少有一个为0
(D) a不为0且b为0, 或b不为0且a为0.
5
命题“若A  B,则A
B,则A C”的否命题是( )
C”的否命题是( )
(A)若A B,则A
B,则A C (B)若A
C (B)若A B, 则A
B, 则A C
C
(C)若A B,则A
B,则A C (D)若A
C (D)若A B,则A
B,则A C
C
6 x 1> 2且x2 > 2是x1+x2 > 4且 x1x2 > 4的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
7如果x在映射f:R → R下的象是x2-1 ,那么3在f下的原象是( )
(A)2 (B)-2 (C)2或 -2 (D)8
8函数f(x)=-x2-2x+3(-5≤x<0)的值域是( )
(A)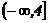 (B)
(B)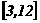 (C)
(C)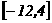 (D)
(D)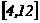
班级____学号____姓名____成绩____
9 函数y=x2+2x(x<-1)的反函数是( )
(A)y= 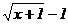 (x<-1) (B)y=
(x<-1) (B)y=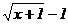 (x>-1)(C)y=-
(x>-1)(C)y=-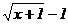 (x<-1) (D)y=-
(x<-1) (D)y=-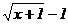 (x>-1)
(x>-1)
10 已知偶函数f(x)的定义域为{ x|x∈R,且x≠0}若f(x)在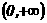 上单调递增,则( )
上单调递增,则( )
(A)f(-1)<f(-2)<f(-3)(B)f(-1)<f(-3)<f(-2)(C)f(-3)<f(-2)<f(-1)(D)f(-2)<f(-1)<f(-3)
11 已知函数y=x2+2(a-2)x+5在区间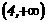 上是增函数,则实数a的取值范围是( )
上是增函数,则实数a的取值范围是( )
(A) a≤-2 (B)a≥-2 (C)a≤-6 (D)a≥-6
12 下列各式正确的是( )
(A)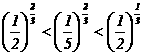 (B)
(B) 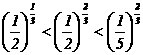
(C)
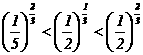 (D)
(D) 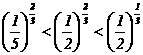
二填空(每小题4分)
13 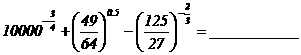
 14 函数f(x)在
14 函数f(x)在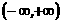 上为奇函数,且x∈
上为奇函数,且x∈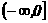 时, f(x)=x(x-1),则当x∈
时, f(x)=x(x-1),则当x∈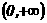 时,f(x)=
时,f(x)=
 15 已知函数f(x)的定义域是
15 已知函数f(x)的定义域是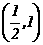 则函数f(2x)的定义域为
则函数f(2x)的定义域为
16 已知f(x)=x2+10x+3当x∈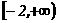 时,f(x)≥a2+2a-16恒成立, 则实数a的取值范围
时,f(x)≥a2+2a-16恒成立, 则实数a的取值范围
 三 解答题
三 解答题
17 集合A={x|x2-x-6>0} ,B={x| |x-1|<a},若A∩B≠Ф,求a的取值范围。(9分)
18画出下列函数图象,并指出函数的单调区间(9分)
①y=|x2-1| ②y=-x2+2|x|+3
19已知定义在区间(-2,2)上的函数f(x),求函数G(x)=f(1+x)+f(1-x2)的定义域 ;当f(x)既是奇函数,又是减函数时, 求
G(x)<0的解(9分)
20已知y1=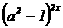 ,y2=
,y2=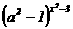 ,x为何值时y1
> y2
(9分)
,x为何值时y1
> y2
(9分)
命题人:田国瑞 尹秀凤 核对人:王树军 孙洪甲 刘玉荣
24、概率(12)
某人忘记了电话号码的最后两个数字,因而他随意拨号.
(1)求第3次接通电话的概率
(2)求拨号不超过3次而接通电话的概率 (3)若最后一个数字是奇数,求拨号不超过3次而接通电话的概率
23、概率(10)
甲乙二人各提一个装有卡片的提包,从中取出卡片来比胜负。甲的提包里有号码为1的卡片2张,号码为3的卡片1张;乙的提包装有号码为1的卡片1张,号码为2的卡片2张。甲、乙同时从自己的提包里每次取出卡片1张相比,取出的不再放回,直到二人取出的卡片号码不相同时,号码大的一方为胜。求甲、乙二人分别获胜的概率。
22、排列组合(10)
从5个男生和3个女生中选5人担任5门不同学科的课代表,求符合下列条件的选法数:(1)女生必须少于男生;(2)某女生担任语文课代表;(3)某男生必须包括在内,但不担任数学课代表;(4)某女生必须担任语文课代表,某男生必须担任课代表,但不担任数学课代表.
21、(二项式定理)(8)
设m,n是正整数,f(x)=(1+x)m+(1+x)n,已知f(x)展开式中,x的系数为19.
(1)当m,n为何值时,x2的系数最小;
(2)当x2的系数最小时,求x7的系数。
20、(立几)(8)
如图,在正四棱柱ABCD-A1B1C1D1中,点E在棱DD1上,截面EAC//D1B,且平面EAC与底面ABCD所成的角为45°,AB=a.
(1)求截面EAC的面积;(2)求异面直线A1B1与AC之间的距离.
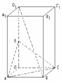
19、(排列组合)(8)
30030能被多少个不同的偶数整除?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com