5、两条异面直线在同一个平面内的射影一定是( 　 )

A 两条相交直线　　　　　　　　　　　 B 两条平行直线　

　C 两条相交直线或两条平行直线　　　　 D 以上都不对

4、若点E、F、G、H顺次为空间四边形ABCD四条边AB、BC、CD、DA的中点，EG=3，FH=4，则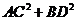的值为( 　 )

A. 25　　　　　　 B. 50　　　　　　　 　C. 100　　　　　 D. 200　　　　　

3、球的体积是π，则此球的表面积是(　)

A. 12π　 　　　　B. 16π　 　　　　　C. π　 　　　D. π

2、给出下列四个命题：

(1)空间四点共面，则其中必有三点共线　　

(2)空间四点不共面，则其中任何三点不共线

(3)空间四点中存在三点共线，则此四点共面　

(4)空间四点中任何三点不共线，则此四点不共面

其中正确的有( 　 )

A．(2)(3)　　　 B(1)(2)(3)　　 C(1)(2)　　 D(2)(3)(4)

1、下列说法不正确的是

A,如果一条直线的两点在一个平面内,则这条直线的所有点都在这个平面内.

B,如果两个平面有一个公共点,则它们还有其他公共点,且它们都在一条直线上.

C,三点确定一个平面.　　　　　　 D,平行于同一条直线的两条直线互相平行

22.(本小题满分14分) 甲、乙两人进行五次比赛，如果甲或乙无论谁胜了三次，比赛宣告结束。假定每次甲获胜的概率是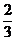，乙获胜的概率是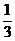，试求下列概率。(I)比赛以甲3胜1败而结束的概率；(II)比赛以乙3胜2败而结束的概率；(III)设最终甲获胜的概率为a，乙获胜的概率为b，求a：b的值。

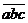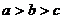21. (本小题满分12分) 三位数，若，则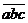称为渐升数，若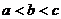，则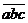为渐降数，若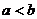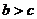，称为凸数，若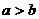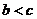，称为凹数，求四种数各有多少个。

20．(本小题满分12分)在一次三人象棋对抗赛里，甲胜乙的概率为0.4，乙胜丙的概率为0.5，丙胜甲的概率为0.6，比赛顺序如下：第一局，甲对乙；第二局，第一局的胜者对丙；第三局，第二局的胜者对第一局的败者；第四局，第三局的胜者对第二局的败者。计算：①乙连胜四局的概率；②丙连胜三局的概率.

19.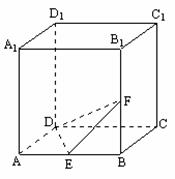 (本小题满分12分)

如图，正方体ABCD－A₁B₁C₁D₁中，E，F分别为AB与BB₁的中点，(1)求证：EF⊥平面A₁D₁B ； (2)求二面角F－DE－C大小．

18．(本小题满分12分)某学校有9名教师，其中4人只能教数学，3人只能教英语，2人既能教数学又能教英语.现要从中选出6人参加讲师团，必须有数学教师和英语教师各3人，有多少种不同的选法？