
题目列表(包括答案和解析)
3.如图,棱锥P-ABCD的高PO=3,截面积A’B’C’D’平行于底面ABCD,PO与截面交于O’,且OO’=2。如果四边形ABCD的面积为36,则四边形A’B’C’D’的面积为 ( )
 A.12 B. 16 C. 4 D. 8
A.12 B. 16 C. 4 D. 8
2.一个棱柱是正四棱柱的条件是 ( )
A.底面是正方形,有两个侧面是矩形
B.底面是正方形,有两个侧面垂直于底面
C.底面是菱形,且有一个顶点处的三条棱两两垂直
D.每个侧面都是全等矩形的四棱柱
1.若正棱锥的底面边长与侧棱长都相等,则该棱锥一定不是 ( )
A.三棱锥 B.四棱锥 C.五棱锥 D.六棱锥
22. 解:(1)因为SB在底面ABC上的射影AB与AD不垂直,否则与AB=AC且D为BC的中点矛盾,所以AD与SB不垂直;(4分)
(2)设 ,则
,则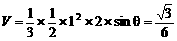
解得 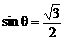 ,所以
,所以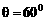 (舍),
(舍),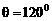 .
.
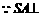 平面ABC,AB=AC,D为BC的中点
平面ABC,AB=AC,D为BC的中点
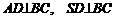 ,
,
则 是二面角S-BC-A的平面角.
是二面角S-BC-A的平面角.
在 中,
中,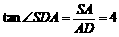 ,
,
故二面角的正切值为4;(9分)
(3)由(2)知, 平面SDA,所以平面SBC
平面SDA,所以平面SBC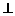 平面SDA,过点A作AE
平面SDA,过点A作AE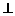 SD,则AE
SD,则AE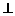 平面SBC,于是点A到平面SBC的距离为AE,
平面SBC,于是点A到平面SBC的距离为AE,
从而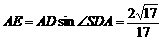 即A到平面SBC的距离为
即A到平面SBC的距离为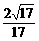 .(14分)
.(14分)
21. (14分).
(Ⅰ)证法一:∵点D是正△ABC中BC边的中点,∴AD⊥BC,
又A1A⊥底面ABC,∴A1D⊥BC ,∵BC∥B1C1,∴A1D⊥B1C1.
证法二:连结A1C1,则A1C=A1B. ∵点D是正△A1CB的底边中BC的中点,
∴A1D⊥BC ,∵BC∥B1C1,∴A1D⊥B1C1.(4分)
(Ⅱ)解法一:作DE⊥AC于E, ∵平面ACC1⊥平面ABC,
∴DE⊥平面ACC1于E,即DE的长为点D到平面ACC1的 距离. 在Rt△ADC中,
AC=2CD=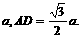
∴所求的距离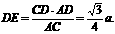 (9分)
(9分)
解法二:设点D到平面ACC1的距离为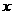 ,
,
∵体积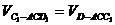
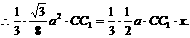
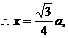 即点D到平面ACC1的距离为
即点D到平面ACC1的距离为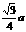 .(9分)
.(9分)
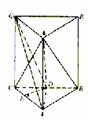
(Ⅲ)答:直线A1B//平面ADC1,证明如下:
证法一:如图1,连结A1C交AC1于F,则F为A1C的中点,∵D是BC的中点,∴DF∥A1B,
又DF 平面ADC1,A1B
平面ADC1,A1B 平面ADC1,∴A1B∥平面ADC1. (14分)
平面ADC1,∴A1B∥平面ADC1. (14分)
证法二:如图2,取C1B1的中点D1,则AD∥A1D1,C1D∥D1B,
∴AD∥平面A1D1B,且C1D∥平面A1D1B,
∴平面ADC1∥平面A1D1B,∵A1B 平面A1D1B,∴A1B∥平面ADC1. (14分)
平面A1D1B,∴A1B∥平面ADC1. (14分)
20.(12分)证明:由题设,有
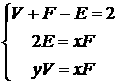
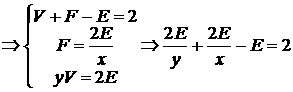 ,
,
由此得到所证等式.
19. 解:设长方体的底面长,宽分别为x,y, 高为z.(2分)
则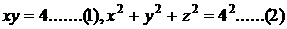
由:(1)、(2),得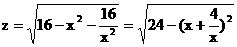 。(4分)
。(4分)
∵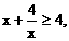 ∴
∴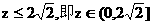 .(6分)
.(6分)
∵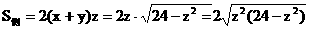 .(8分)
.(8分)
将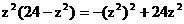 的二次函数视为
的二次函数视为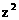 的二次函数,它的增区间是[0,12].(10分)由于
的二次函数,它的增区间是[0,12].(10分)由于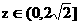 ,故当
,故当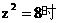 ,
,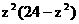 取最大值128.
取最大值128.
∴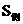 的最大值为
的最大值为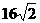 .(12分)
.(12分)
 17. 解: 如图, 四面体ABCD中,AB=BC=CA=1(2分), DA=DC=
17. 解: 如图, 四面体ABCD中,AB=BC=CA=1(2分), DA=DC=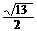 (4分), 只有棱DB的长x是可变的. 在三角形ACD中, M为AC的中点, MD=
(4分), 只有棱DB的长x是可变的. 在三角形ACD中, M为AC的中点, MD=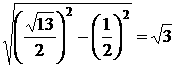 . MB=
. MB=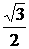 (6分).
(6分).
由MF-MB<BD<MD+MB(8分), (MF=MD)
得: 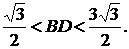 (10分)
(10分)
18. 解:用直尺测出木板的长为a,宽为b,知道a>b>0,又知道两墙面所成二面角为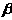 (2分).
(2分).
设b作底边,a作直三棱柱的侧棱,底面另两边为x,y, 则
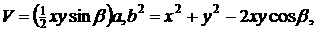 (4分)
(4分)
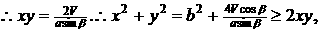 (6分)
(6分)
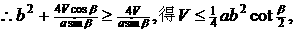 (8分)
(8分)
则当x=y时,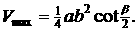 (10分)同理,若a作底边,有
(10分)同理,若a作底边,有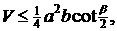 当x=y时,
当x=y时,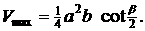
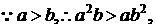 ∴
∴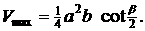
所以把长边放在底面,短边作侧棱,且围成底面是等腰三角形时,容积最大。(12分)
 13.
13.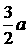 14.
14.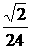 15.
15.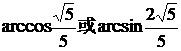 16.AC⊥BD,或AB=AD且BC=DC
16.AC⊥BD,或AB=AD且BC=DC
13.解:
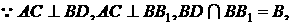
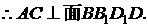
设AC∩BD=O,则AO=CO. ∴平面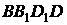 是线段AC的垂直平分面,∴C是A关于平面
是线段AC的垂直平分面,∴C是A关于平面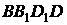 的对称点。连CE交面
的对称点。连CE交面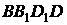 于M ,则M 就是要求的点,这时AM+ME 最小。又AM=CM, ∴AM+ME的最小值就是CE 的长,而
于M ,则M 就是要求的点,这时AM+ME 最小。又AM=CM, ∴AM+ME的最小值就是CE 的长,而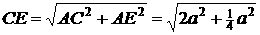 =
=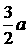 , ∴AM+ME的最小值为
, ∴AM+ME的最小值为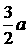 .
.
12. 易得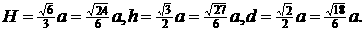 ∴
∴ 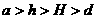 .选B.
.选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com