4．A、B、C为已知直线上的三个定点，动点P不在此直线上，且使∠APB=∠BPC，求动点P的轨迹．

作业答案：

3．等腰三角形的顶点是A(4，2)，底边一个端点是B(3，5)，求另一个端点的轨迹方程，并说明它的轨迹是什么．

2．求经过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点，并且圆心在直线x-y-4=0上的圆的方程．

1．求下列各圆的一般方程：

(1)过点A(5，1)，圆心在点C(8，-3)；

(2)过三点A(-1，5)、B(5，5)、C(6，-2)．

(五)小结

1．圆的一般方程的定义及特点；

2．用配方法求出圆的圆心坐标和半径；

3．用待定系数法，导出圆的方程．

(四)应用与举例

同圆的标准方程(x-a)2+(y-b)2=r2一样，方程x2+y2+Dx+Ey+F=0也含有三个系数D、E、F，因此必具备三个独立的条件，才能确定一个圆．下面看一看它们的应用．

例1　 求下列圆的半径和圆心坐标：

(1)x2+y2-8x+6y=0，

(2)x2+y2+2by=0．

此例由学生演板，教师纠错，并给出正确答案：(1)圆心为(4，-3)，半径为5；(2)圆心为(0，-b)，半径为|b|，注意半径不为b．

同时强调：由圆的一般方程求圆心坐标和半径，一般用配方法，这要熟练掌握．

例2　 求过三点O(0，0)、A(1，1)、B(4，2)的圆的方程．

解：设所求圆的方程为x2+y2+Dx+Ey+F=0，由O、A、B在圆上，则有

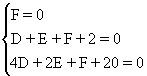
解得：D=-8，E=6，F=0，

故所求圆的方程为x2+y2-8x+6=0．

例2小结：

1．用待定系数法求圆的方程的步骤：

(1)根据题意设所求圆的方程为标准式或一般式；

(2)根据条件列出关于a、b、r或D、E、F的方程；

(3)解方程组，求出a、b、r或D、E、F的值，代入所设方程，就得要求的方程．

2．关于何时设圆的标准方程，何时设圆的一般方程：一般说来，如果由已知条件容易求圆心的坐标、半径或需要用圆心的坐标、半径列方程的问题，往往设圆的标准方程；如果已知条件和圆心坐标或半径都无直接关系，往往设圆的一般方程．再看下例：

例3　 求圆心在直线 l：x+y=0上，且过两圆C1∶x2+y2-2x+10y-24=0和C2∶x2+y2+2x+2y-8=0的交点的圆的方程．

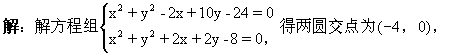
(0，2)．

设所求圆的方程为(x-a)2+(y-b)2=r2，因为两点在所求圆上，且圆心在直线l上所以得方程组为

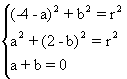
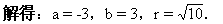
故所求圆的方程为：(x+3)2+(y-3)2=10．

这时，教师指出：

(1)由已知条件容易求圆心坐标、半径或需要用圆心的坐标、半径列方程的问题，往往设圆的标准方程．

(2)此题也可以用圆系方程来解：

设所求圆的方程为：

x2+ y2-2x+10y-24+λ(x2+y2+2x+2y-8)=0(λ≠-1)

整理并配方得：

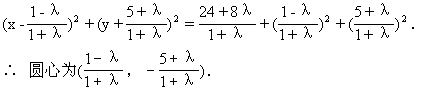
由圆心在直线l上得λ=-2．

将λ=-2代入所假设的方程便可得所求圆的方程为x2+y2+6x-6y+8=0．此法到圆与圆的位置关系中再介绍，此处为学生留下悬念．

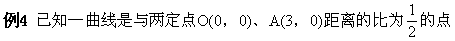
的轨迹，求这个曲线的方程，并画出曲线．

此例请两位学生演板，教师巡视，并提示学生：

(1)由于曲线表示的图形未知，所以只能用轨迹法求曲线方程，设曲线上任一点M(x，y)，由求曲线方程的一般步骤可求得；

(2)应将圆的一般方程配方成标准方程，进而得出圆心坐标、半径，画出图形．

(三)圆的一般方程的特点

请同学们分析下列问题：

问题：比较二元二次方程的一般形式

Ax2+Bxy+Cy2+Dx+Ey+F=0．

(2)

与圆的一般方程

x2+y2+Dx+Ey+F=0，(D2+E2-4F＞0)．

(3)

的系数可得出什么结论？启发学生归纳结论．

当二元二次方程 Ax2+Bxy+Cy2+Dx+Ey+F=0具有条件：

(1)x2和y2的系数相同，不等于零，即A=C≠0；

(2)没有xy项，即B=0；

(3)D2+E2-4AF＞0．

它才表示圆．条件(3)通过将方程同除以A或C配方不难得出．

教师还要强调指出：

(1)条件(1)、(2)是二元二次方程(2)表示圆的必要条件，但不是充分条件；

(2)条件(1)、(2)和(3)合起来是二元二次方程(2)表示圆的充要条件．

(二)圆的一般方程的定义

1．分析方程x3+y2+Dx+Ey+F=0表示的轨迹

将方程x2+y2+Dx+Ey+F=0左边配方得：

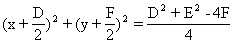
(1)

(1)当D2+E2-4F＞0时，方程(1)与标准方程比较，可以看出方程

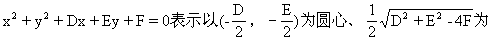
半径的圆；

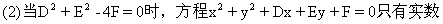
(3)当D2+E2-4F＜0时，方程x2+y2+Dx+Ey+F=0没有实数解，因而它不表示任何图形．

这时，教师引导学生小结方程x2+y2+Dx+Ey+F=0的轨迹分别是圆、

法．

2．圆的一般方程的定义

当D2+E2-4F＞0时，方程x2+y2+Dx+Ey+F=0称为圆的一般方程．

(一)复习引入新课

前面，我们已讨论了圆的标准方程(x-a)2+(y-b)2=r2，现将展开可得x2+y2-2ax-2by+a²+b2-r2=0．可见，任何一个圆的方程都可以写成x2+y2+Dx+Ey+F=0．请大家思考一下：形如x2+y2+Dx+Ey+F=0的方程的曲线是不是圆？下面我们来深入研究这一方面的问题．复习引出课题为“圆的一般方程”．

讲授、提问、归纳、演板、小结、再讲授、再演板．