
题目列表(包括答案和解析)
3.如下图可作为y=f(x)的图象的是
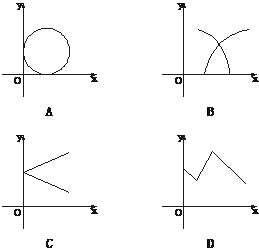
解析:在A、B、C中,均存在一个x对应两个y的情况,因此A、B、C均错.
答案:D
2.若函数y=f(x)的定义域是[-2,4],则函数g(x)=f(x)+f(-x)的定义域是
A.[-4,4] B.[-2,2] C.[-4,-2] D.[2,4]
解析:要使函数有意义,只需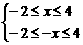
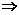
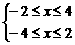
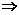 -2≤x≤2,
-2≤x≤2,
即函数的定义域是[-2,2].
答案:B
1.已知集合A=B=R,x∈A,y∈B,f:x→y=ax+b,若4和10的原象分别对应6和9,则19在f作用下的象为
A.18 B.30 C.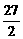 D.28
D.28
解析:由题意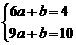
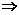 a=2,b=-8,
a=2,b=-8,
∴对应法则为y=2x-8.
故19在f作用下的象是y=2×19-8=30.
答案:B
[例5]
如图,已知底角为45°的等腰梯形ABCD,底边BC长为7 cm,腰长为2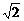 cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
cm,当一条垂直于底边BC(垂足为F)的直线l从左至右移动(与梯形ABCD有公共点)时,直线l把梯形分成两部分,令BF=x,试写出左边部分的面积y与x的函数解析式,并画出大致图象.
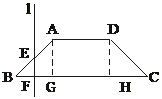
分析:要注意动直线在移动的过程中所围成的几何体的形状及相应图形的面积公式.
解:过点A、D分别作AG⊥BC,DH⊥BC,垂足分别是G、H.
因为ABCD是等腰梯形,底角为45°,AB=2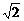 cm,
cm,
所以BG=AG=DH=HC=2 cm.
又BC=7 cm,所以AD=GH=3 cm.
(1)当点F在BG上,即x∈(0,2]时,y=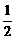 x2;
x2;
(2)当点F在GH上,即x∈(2,5]时,y=2+(x-2)·2=2x-2;
(3)当点F在HC上,即x∈(5,7]时,
y=S五边形ABFED=S梯形ABCD-SRt△CEF=-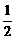 (x-7)2+10.
(x-7)2+10.
所以,函数解析式为y=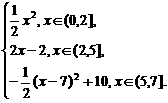
图象如图.
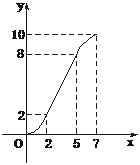
评注:在函数定义域内,对自变量x的不同取值范围有着不同的对应法则,这样的函数叫做分段函数.它的图象可以是直线、射线、线段、折线、连续的曲线、离散的点等.要不断尝试用数学表达式去表达实际问题.
●试题详解
高中同步测控优化训练(五)
第二章 函数(一)(A卷)
说明:本试卷分为第Ⅰ、Ⅱ卷两部分,请将第Ⅰ卷选择题的答案填入题后括号内,第Ⅱ卷可在各题后直接作答.共100分,考试时间90分钟.
第Ⅰ卷(选择题 共30分)
[例4]
设函数f(x)=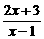 ,已知函数y=g(x)的图象与y=f--1(x+1)的图象关于直线y=x对称,求g(3)的值.
,已知函数y=g(x)的图象与y=f--1(x+1)的图象关于直线y=x对称,求g(3)的值.
分析一:f(x)→f-1(x)→f-1(x+1)→g(x)→g(3).
解法一:由y=f(x)= 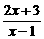 ,得f--1(x)=
,得f--1(x)=
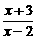 ,
,
∴f--1(x+1)= 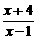 .
.
又∵y=g(x)与y=f--1(x+1)的图象关于直线y=x对称,
∴y=g(x)=f--1[f--1(x+1)]=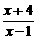 .
.
∴g(3)= 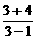 =
=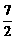 .
.
分析二:因为f--1(x+1)与f(x)和g(x)均有联系,所以借助f--1(x+1)直接找到g(x)与f(x)的关系.
解法二:由y=f--1(x+1),得x+1=f(y),
∴x=f(y)-1.
∴y=f--1(x+1)的反函数为y=g(x)=f(x)-1.
∴g(3)=f(3)-1=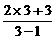 -1=
-1=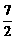 .
.
分析三:利用f(a)=b f--1(b)=a.
f--1(b)=a.
解法三:设g(3)=t,则g-1(t)=3,
∵g-1(x)=f--1(x+1),
∴f--1(t+1)=3.∴f(3)=t+1,t=f(3)-1=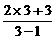 -1=
-1=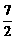 ,即g(3)=
,即g(3)= 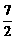 .
.
评注:在求解与反函数有关的问题时,要充分利用原函数与反函数性质、图象间的关系.本题中注意不要将y=f--1(x+1)的反函数误认为y=f(x+1).
[例2] (1)已知f(x)的定义域为[1,2),求函数f(x2)的定义域;
(2)已知f(x+1)的定义域为[0,1],求函数f(x)的定义域.
解:(1)由f(x)的定义域为[1,2),
可知f(x2)中自变量x2也应在[1,2)中,
故1≤x2<2,∴-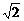 <x≤-1或1≤x<
<x≤-1或1≤x<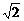 ,
,
即f(x2)的定义域为(-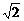 ,-1]∪[1,
,-1]∪[1, 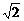 ).
).
(2)已知f(x)的定义域为[0,1],即0≤x≤1,
则1≤x+1≤2,∴f(x)的定义域为[1,2].
点评:该类问题关键在于正确理解函数概念,要理解定义域为自变量x的取值集合.一般地,已知f(x)的定义域为D,求f[g(x)]的定义域时,令g(x)∈D,解得x的取值范围即为f[g(x)]的定义域;已知f[g(x)]的定义域为D,求f(x)的定义域时,可由x的取值范围求得g(x)的值域,即为f(x)的定义域.
[例3]
设函数f(x)= 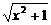 -ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
-ax,其中a>0,求a的取值范围,使函数f(x)在[0,+∞)上为单调函数.
解:任取x1、x2∈[0,+∞)且x1<x2,则
f(x1)-f(x2)=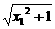 -
-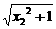 -a(x1-x2)
-a(x1-x2)
=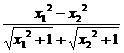 -a(x1-x2)
-a(x1-x2)
=(x1-x2)(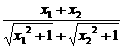 -a).
-a).
(1)当a≥1时,∵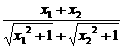 <1,
<1,
又∵x1-x2<0,
∴f(x1)-f(x2)>0,即f(x1)>f(x2).
∴a≥1时,函数f(x)在区间[0,+∞)上为减函数.
(2)当0<a<1时,在区间[0,+∞)上存在x1=0,x2=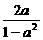 ,满足f(x1)=f(x2)=1,
,满足f(x1)=f(x2)=1,
∴0<a<1时,f(x)在[0,+∞)上不是单调函数.
评注: ①判断单调性常规思路为定义法;②变形过程中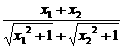 <1利用了
<1利用了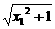 >|x1|≥x1,
>|x1|≥x1, 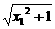 >x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
>x2这个结论;③从a的范围看还需讨论0<a<1时f(x)的单调性,这也是数学严谨性的体现.
[例1]
已知f(x)=4x2-2x+1,g(x)=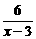 ,求f(
,求f(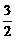 ),f(-x),g(
),f(-x),g(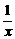 ),f[g(x)],g[f(x)].
),f[g(x)],g[f(x)].
解:f(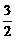 )=4(
)=4(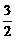 )2-2·
)2-2·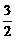 +1=7,
+1=7,
f(-x)=4·(-x)2-2(-x)+1=4x2+2x+1,
g(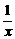 )=
)=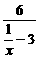 =
=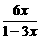 ,
,
f[g(x)]=4[g(x)]2-2[g(x)]+1
=4·(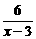 )2-2·
)2-2·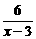 +1
+1
=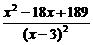 ,
,
g[f(x)]=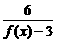 =
=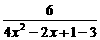
=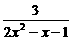 .
.
评注:本题是已知f、g这两个对应法则,求它们的一些函数值或由它们构造的复合函数(值).这类问题只要将自变量x或其代数式直接代入即可解决.若已知的是由两个函数复合而成的复合函数以及其中一个函数,那么怎样去求另一个函数呢?常见的方法有:待定系数法、拼凑法、换元法及消去法等.
●知识网络
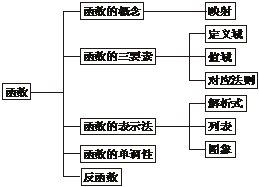
●范题精讲
19.(本小题满分12分)济南市某电脑公司在市区和微山湖各有一分公司,市区分公司现有电脑6台,微山湖分公司有同一型号的电脑12台.淄博某单位向该公司购买该型号电脑10台,济南某单位向该公司购买该型号电脑8台,已知市区运往淄博和济南每台电脑的运费分别是40元和30元,微山湖运往淄博和济南每台电脑的运费分别是80元和50元.
(1)设从微山湖调运x台至淄博,该公司运往淄博和济南的总运费为y元,求y关于x的函数关系式.
(2)若总运费不超过1000元,问能有几种调运方案?
(3)求总运费最低的调运方案及最低运费.
解:(1)若微山湖调运x台至淄博,则运(12-x)台至济南,市区运(10-x)台至淄博,运往济南6-(10-x)=(x-4)台(4≤x≤10,x∈N),
则y=80x+50(12-x)+40(10-x)+30(x-4)
=20x+880,
所以y=20x+880(x∈N,且4≤x≤10).
(2)由y≤1000,得20x+880≤1000,解得x≤6.
又因为x∈N,且4≤x≤6,所以x=4、5、6,
即有3种调运方案.
(3)因为y为增函数,所以当x=4时,ymin=960.
故从微山湖运4台至淄博,运8台至济南,市区运6台至淄博,运费最低.
18.(本小题满分12分)有甲、乙两种商品,经营销售这两种商品所能获得的利润依次是P和Q(万元),它们与投入资金x(万元)的关系有经验公式:P=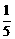 x,Q=
x,Q=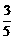
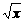 .今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
.今有3万元资金投入经营甲、乙两种商品,为获得最大利润,对甲、乙两种商品的资金投入分别应为多少,能获得的最大利润为多少?
解:设对甲种商品投资x万元,获总利润为y万元,则对乙种商品的投资为(3-x)万元,于是y=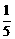 x+
x+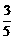
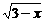 (0≤x≤3).
(0≤x≤3).
令t=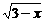 (0≤t≤
(0≤t≤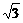 ),则x=3-t2,
),则x=3-t2,
∴y=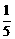 (3-t2)+
(3-t2)+ 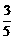 t=
t=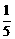 (3+3t-t2)
(3+3t-t2)
=-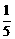 (t-
(t-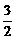 )2+
)2+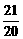 ,t∈[0,
,t∈[0,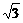 ].
].
∴当t=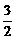 时,ymax=
时,ymax=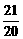 =1.05(万元);
=1.05(万元);
由t=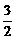 可求得x=0.75(万元),
可求得x=0.75(万元),
3-x=2.25(万元),
∴为了获得最大利润,对甲、乙两种商品的资金投入应分别为0.75万元和2.25万元,获得最高利润1.05万元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com