
题目列表(包括答案和解析)
5.10名学生计划“五一”这天去郊游,本着自愿的原则,规定任何人可以“去”或“不去”,则这10名学生“五一”这天去郊游的情况共有( )
A.C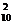 种 B.A
种 B.A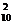 种 C.102种 D.210种
种 C.102种 D.210种
4.一个正四棱锥的底面面积为Q,则它的中截面的边长是( )
A.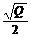 B.
B.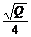 C.
C.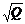 D.
D.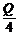
3.某气象站天气预报的准确率为80%,则5次预报中至少有4次准确的概率(结果保留两位有效数字)是( )
A.0.23 B.0.41 C.0.74 D.0.67
2.α表示一个平面,l表示一条直线,则α内至少有一条直线与直线l ( )
A.平行 B.相交 C.异面 D.垂直
1.C520+C420+C421=( )
A.C521 B.C422 C.C522 D.C421
21.解:设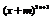 的通项公式为
的通项公式为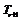 ,则
,则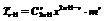 .令
.令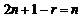 ,得
,得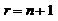 故此展开式中
故此展开式中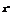 项的系数为
项的系数为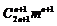 由题意知:
由题意知: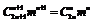
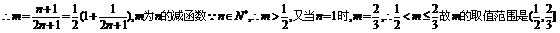
22(I)  为平行四边形,连结AC交DE于O,可证
为平行四边形,连结AC交DE于O,可证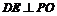 且
且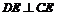 ,
,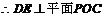
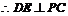 .
.
(II)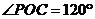 ,
,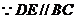 ,
,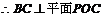
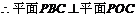 ,作
,作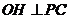 ,则
,则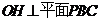 ,又
,又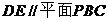 ,
,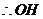 为所求的距离,
为所求的距离,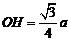 ;
;
(III)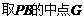 ,连
,连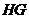 ,可知
,可知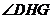 为所求二面角,
为所求二面角,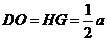 ,
,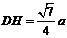 ,求得
,求得
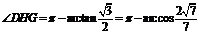 .
.
欢迎访问
18 (I)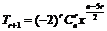 ,由
,由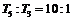 ,得
,得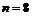 ;(II)令
;(II)令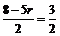 ,得
,得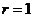 ,故
,故 ;
;
19(I)以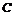 为原点建系,易得
为原点建系,易得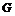 是
是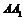 的中点;(II)平面
的中点;(II)平面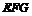 的一个法向量为
的一个法向量为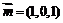 ,则
,则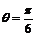 .
.
20.解:(1)∵ABB1A1是菱形,∠A1AB=60°,且M为A1B1的中点,
∴BM⊥A1B1, …………2分
又A1B1∥AB,∴MB⊥AB.平面ABB1A1⊥平面ABC,
∴MB⊥平面ABC.
又AC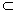 平面ABC,∴BM⊥AC. …………6分
平面ABC,∴BM⊥AC. …………6分
(2)作CN⊥AB于N,由于△ABC为正三角形,知N为AB为中点,又平面ABB1A1⊥平面ABC,∵CN⊥平面A1ABB1,作NE⊥MB于E点,连CE,由三垂线定理可知CE⊥BM, ∴∠NEC为二面角A1-BM-C的平面角.………9分
由题意可知CN=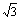 ,在Rt△CNE中,
,在Rt△CNE中,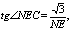 要∠NEC最小,只要NE取最大值.
要∠NEC最小,只要NE取最大值.
又∵△A1B1B为正三角形,∴当M为A1B1中点时,MB⊥平面ABC,即E与B重合.
此时NE取最大值且最大值为1,∴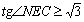 .
.
∴∠NEC的最小值为60°,……10分
此时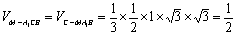 .……14分
.……14分
22.(本小题满分12分)
如图,梯形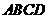 中,
中,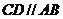 ,
,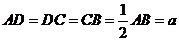 ,
, 是
是 的中点,将
的中点,将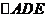 沿
沿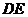 折起,使点
折起,使点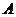 折到点
折到点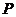 的位置,且二面角
的位置,且二面角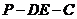 的大小为
的大小为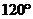 .
.
(I)求证: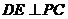 ;
;
(II)求点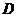 到平面
到平面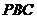 的距离;
的距离;
(III)求二面角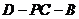 的大小.
的大小.
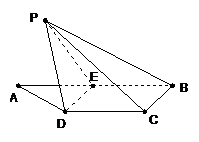
DDCB? ?DDBD ? 150 
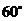
? 3
21.(本小题满分12分)已知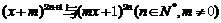 的展开式中含
的展开式中含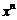 项的系数相等,求实数
项的系数相等,求实数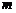 的取值范围.
的取值范围.
19.(本小题满分13分)在直三棱柱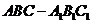 中,
中,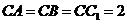 ,
,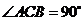 ,
,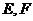 分别是
分别是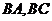 的中点,
的中点,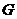 是
是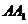 上一点,且
上一点,且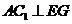 .
.
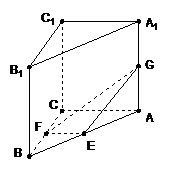 (I)求
(I)求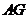 的长;
的长;
(II)求直线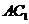 与平面
与平面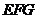 所成的角
所成的角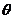 的大小.
的大小.
20(本小题满分13分) 如图,三棱柱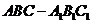 的底面是边长为2的等边三角形,侧面
的底面是边长为2的等边三角形,侧面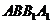 是
是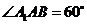 的菱形,且平面
的菱形,且平面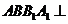 平面
平面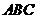 ,点
,点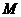 是
是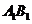 上的动点.
上的动点.
(I)当点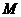 是
是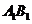 的中点时,求证:
的中点时,求证: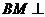 面
面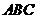 ;
;
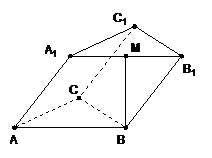 (II)当二面角
(II)当二面角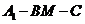 的平面角最小时, 求三棱锥
的平面角最小时, 求三棱锥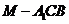 的体积.
的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com