
题目列表(包括答案和解析)
3.当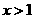 时,不等式
时,不等式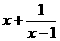 ≥a恒成立, 则实数a的取值范围是 ( )
≥a恒成立, 则实数a的取值范围是 ( )
(A)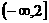 (B)
(B)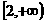 (C)
(C)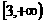 (D)
(D)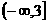
2.已知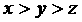 且
且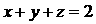 ,则下列不等式中恒成立的是( )
,则下列不等式中恒成立的是( )
(A)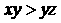 (B)
(B)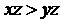 (C)
(C)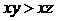 (D)
(D)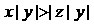
1.对“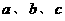 是不全相等的正数”,给出下列判断:
是不全相等的正数”,给出下列判断:
①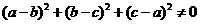 ; ②
; ②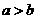 与
与 及
及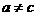 中至少有一个成立;
中至少有一个成立;
③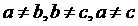 不能同时成立.其中判断正确的个数为( )
不能同时成立.其中判断正确的个数为( )
(A)0个 (B)1个 (C)2个 (D)3个
12.依题意p, q中真假情况为:一真一假,p真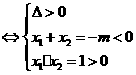
 m>2,q真
m>2,q真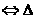 <0
<0 1<m<3,⑴若p假q真,则
1<m<3,⑴若p假q真,则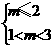
 1<m≤2;⑵若p真q假,则
1<m≤2;⑵若p真q假,则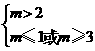
 m≥3;综上所述, 实数
m≥3;综上所述, 实数 的取值范围为(1,2]∪[3,+∞).
的取值范围为(1,2]∪[3,+∞).
11.法一:假设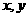 均小于1,由不等式同向相加的性质知x+y<2即
均小于1,由不等式同向相加的性质知x+y<2即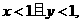
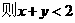 ,这说明原命题的逆否命题成立.∴原命题成立.
,这说明原命题的逆否命题成立.∴原命题成立.
法二:(反证法)假设x<1且y<1,由不等式同向相加的性质x+y<2与已知x+y≥2矛盾,∴ 假设不成立,∴ x、y中至少有一个不小于1.
[注]反证法的理论依据是:欲证“若p则q”为真,先证“若p则非q”为假,因在条件p下,q与非q是对立事件(不能同时成立,但必有一个成立),所以当“若p则非q”为假时,“若p则q”一定为真.
12.已知命题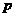 :方程
:方程 有两个不等的负实根;命题
有两个不等的负实根;命题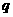 :方程
:方程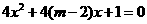 无实根, 若“
无实根, 若“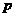 或
或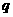 ”为真,而“
”为真,而“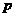 且
且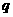 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
高二数学上学期期末复习训练(四)答案(常用逻辑用语单元)
ABCCC DC 8.①②④ 9.[0,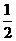 ]
10.
]
10.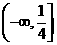
11.已知x、y∈R,x+y≥2,求 证: x、y中至少有一个不小于1.
8.____________; 9.__________; 10.____________;
10.关于x的方程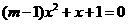 在
在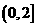 内有解,则实数m的取值范围是_____.
内有解,则实数m的取值范围是_____.
班别___________、学号______、姓名___________
9.设p: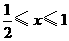 ; q:
; q: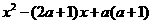 ≤0, 若Øp是Øq的必要而不充分的条件,则实数a的取值范围是
.
≤0, 若Øp是Øq的必要而不充分的条件,则实数a的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com